Solved Examples: Index Numbers and Applications

Solve all questions
Show all work
Unless specified otherwise:
(a.) round all final answers of percentages to the nearest tenth.
(b.) round all final answers of currencies to the nearest cent/hundredth.
(c.) do not round intermediate calculations.

As at today: 02/12/2023, the average annual Consumer Price Index (CPI) from 1913 till 2022 is taken from the United States Bureau of Labor Statistics
(Source: Pages 3 – 5 in Historical Consumer Price Index for All Urban Consumers (CPI-U): U.S. city average, all items, index averages [1982-84=100, unless otherwise noted])
Please focus on these two columns: Year and Annual avg. on Pages 3 – 5

(1.) Use the Consumer Price Index Table.
Presently, the Consumer Price Index (CPI) is published with a reference value of 100 for the years 1982 – 1984.
Assume the CPI were recalculated with 1995 as the reference year.
What would the CPI for 2006 be? Explain your reasoning.

Using 1982 – 1984 as the reference year, the CPI for 2006 = 201.6
Using 1995 as the reference year, the reference value = 152.4
The CPI for 2006 will be:

$ CPI\;\;for\;\;2006 = \dfrac{value}{reference\;\;value} * 100 \\[5ex] = \dfrac{201.6}{152.4} * 100 \\[5ex] = 132.2834646 \\[3ex] 132.3 \lt 201.6 \\[3ex] $ This new CPI (CPI for 2006 using 1995 as the reference year) is less than the initial CPI (CPI for 2006 using 1982–1984 as the reference year)
The new index: 152.4 (the CPI for 1995) is greater than 100 (the average of the CPIs for 1982–1984)

(2.) Over the past three decades, the cost of college has increased at a much greater rate than the CPI.
What does this mean for the average family?

College has become more difficult to afford.
Using the same years as the CPI for reference values, an index of the cost of college would be greater than the CPI.

(3.) Decide whether the following statement makes sense or does not make sense. Explain your reasoning.
An 18th-century philosopher once said, "A penny saved is a penny earned," but if he were alive today, he would be talking about a dollar rather than a penny.

A. The statement does not make sense.
Due to inflation, a penny in the 18th century has less purchasing power than a penny today.

B. The statement does not make sense.
The value of a penny is always 1 cent.

C. The statement makes sense.
Due to inflation, a penny in the 18th century has about the same purchasing power as a dollar today.

D. The statement makes sense.
Due to inflation, a penny in the 18th century has less purchasing power than a penny today.

C. The statement makes sense.
Due to inflation, a penny in the 18th century has about the same purchasing power as a dollar today.

(4.) Assume the current cost of gasoline is 3.50 per gallon.
Determine the current price index number, using the 1975 price of 56.7 cents as the reference value.

$ 56.7\;cents = \dfrac{56.7}{100}\;dollars = 0.567\;dollars \\[5ex] current\;\;price\;\;index\;\;number = \dfrac{current\;\;value}{reference\;\;value} * 100 \\[5ex] = \dfrac{3.5}{0.567} * 100 \\[5ex] = 617.2839506 \\[3ex] \approx 617.3 $

(5.) Given the table of the average gasoline prices, assume it costs $15 to fill a gas tank in 2000, how much would it have cost to fill the same tank in 1970?
Use 2000 as the reference year.

Average Gasoline Prices (per gallon)
Year	Price
1960 1970 1980 1990 2000 2010	$0.31 $0.36 $1.22 $1.23 $1.56 $2.84

1st Approach: Fast Proportional Reasoning

Year	Average Gasoline Prices (per gallon)	Cost to fill a gas tank ($)
1970	0.36	what
2000	1.56	15

$ 1.56 * what = 0.36 * 15 \\[3ex] what = \dfrac{0.36(15)}{1.56} \\[5ex] what = \dfrac{5.4}{1.56} \\[5ex] what = 3.461538462 \\[3ex] what \approx \$3.46 \\[3ex] $ 2nd Approach: Formula/Proportional Reasoning
Price as how many times as the 2000 Price

$ = \dfrac{1970\;\;price\;\;value}{reference\;\;value} \\[5ex] = \dfrac{0.36}{1.56} \\[5ex] = 0.2307692308 \\[3ex] \implies \\[3ex] \dfrac{1970\;\;price}{2000\;\;price} = \dfrac{0.2307692308}{1} \\[5ex] $

Proportional Reasoning Method
1970	2000
0.2307692308	1
what	15

$ what * 1 = 15 * 0.2307692308 \\[3ex] what = 3.461538462 \\[3ex] $ Assume it costs $15 to fill a gas tank in 2000, it would have cost $3.46 to fill the same tank in 1970

(6.) Nicodemus used an average of $17000 to maintain a particular standard of living in 1975.
How much would he have needed in 2001 to maintain the same standard of living?
Assume that all prices have risen at the same rate as the CPI.
Use the CPI table.

1st Approach: Fast Proportional Reasoning

Year	CPI	Average Cost ($)
1975	53.8	17000
2001	177.1	what

$ 53.8 * what = 177.1 * 17000 \\[3ex] what = \dfrac{177.1 * 17000}{53.8} \\[5ex] what = \dfrac{3010700}{53.8} \\[5ex] what = 55960.96654 \\[3ex] what \approx \$55960.97 \\[3ex] $ 2nd Approach: Formula/Proportional Reasoning
Even though the reference years for the CPI table are 1982–1984, we shall use 1975 as the reference year because we are given a value ($17,000 in 1975) to find its worth in 2001.
So, the value is the CPI for 2001 and the reference value is the CPI for 1975.

$ = \dfrac{2001\;\;CPI}{reference\;\;value} \\[5ex] = \dfrac{177.1}{53.8} \\[5ex] = 3.291821561 \\[3ex] \implies \\[3ex] \dfrac{2001\;\;CPI}{1975\;\;CPI} = \dfrac{3.291821561}{1} \\[5ex] $

Proportional Reasoning Method
1975	2001
1	3.291821561
17000	what

$ what * 1 = 17000 * 3.291821561 \\[3ex] what = 55960.96654 \\[3ex] $ Nicodemus would have needed $55,960.97 in 2001 to maintain the same standard of living

(7.) Given the table of the average gasoline prices, assume it costs $15 to fill a gas tank in 2000, how much of the same tank could be filled with $15 in 2010?
Round to two decimal places as needed.
Based on the table, the reference year is 1970.

Average Gasoline Prices (per gallon)
Year	Price
1960 1970 1980 1990 2000 2010	$0.31 $0.36 $1.22 $1.23 $1.56 $2.84

1st Approach: Fast Proportional Reasoning
We will need to do this approach two times.
Because the question is asking what $15 can do for the years: 2000 and also for 2010
So, we begin with substituting $15 for year 2000 because it is used to fill a gas tank in the year 2000
In other words, let us find the equivalent of $15 in 2000, in 2010
In other words, let us find how much is used to fill a gas tank in year 2010

1st time:

Year	Average Gasoline Prices (per gallon)	Cost to fill a gas tank ($)
2000	1.56	15
2010	2.84	what

$ 1.56 * what = 2.84 * 15 \\[3ex] what = \dfrac{2.84 * 15}{1.56} \\[5ex] what = \dfrac{42.6}{1.56} \\[5ex] what = 27.30769231 \\[3ex] $ This means that $27.30769231 is used to fill a gas tank in year 2010
The question wants us to find how much gas tank could be filled with $15 in 2010

2nd time:

Year	Cost to fill ($)	How much gas tank
2010	27.30769231	1
2010	15	what

$ 27.30769231 * what = 15 * 1 \\[3ex] what = \dfrac{15 * 1}{27.30769231} \\[5ex] what = \dfrac{15}{27.30769231} \\[5ex] what = 0.5492957746 \\[3ex] what \approx 0.55 \\[3ex] $ 2nd Approach: Formula/Proportional Reasoning
Based on the table, the reference year is 1970
However, the question has nothing to do with 1970
The years we are concerned with are: 2000 and 2010
Because we are given a value for 2000 ($15) and asked to compare the worth of that value for 2010, we shall use 2000 as the reference year.
This implies that our reference value is $1.56
To solve this question, first: let us find how much $15 in 2000 is worth in 2010
Then, second: if it takes that price (the 'worth' price in 2010) to fill a gallon of gas, how much amount/gallon of gas would be filled with $15?

First: Price as how many times as the 2000 Price

$ = \dfrac{2010\;\;price\;\;value}{reference\;\;value} \\[5ex] = \dfrac{2.84}{1.56} \\[5ex] = 1.820512821 \\[3ex] \implies \\[3ex] \dfrac{2010\;\;price}{2000\;\;price} = \dfrac{1.820512821}{1} \\[5ex] $

Proportional Reasoning Method
2000	2010
1	1.820512821
15	what

$ what * 1 = 15 * 1.820512821 \\[3ex] what = 27.30769231 \\[3ex] $ This means that: $15 in the year 2000 is the same as $27.31 in the year 2010
This means that: if $15 in the year 2000 fills a gas tank, then $27.31 in the year 2010 would fill the same gas tank.
Let us now focus on the year 2010.

Second: So, if it takes $27.30769231 to fill a gas tank in 2010, how much of the tank would be filled with $15 in 2010?

Proportional Reasoning Method
2010	2010
27.30769231	1
15	what

$ what * 27.30769231 = 15 * 1 \\[3ex] what = \dfrac{15}{27.30769231} \\[5ex] what = 0.5492957746 \\[3ex] $ About 0.55 of the same tank could be filled with $15 in 2010.

(8.) Decide whether the following statement makes sense or does not make sense. Explain your reasoning.
When we chart the price of milk in 1995 dollars we find that it has become slightly more expensive, but when we chart it in 1975 dollars we find that it has become cheaper.

A. The statement makes sense because 1975 dollars are worth more than 1995 dollars.
B. The statement makes sense because 1995 dollars are worth more than 1975 dollars.
C. The statement does not make sense because prices always rise with time.
D. The statement does not make sense because the same trend would be seen regardless of what kind of dollars are used.

D. The statement does not make sense because the same trend would be seen regardless of what kind of dollars are used.

(9.) The following table shows a housing index that can be used to compare housing prices in different cities.
Monica sees a house valued at $260,000 in City J.
Determine the price of a comparable house in City A, City H, and City D.

City	Index		City	Index
City A City B City C City D City E	153 123 100 129 99		City F City G City H City J City K	147 150 366 189 400

1st Approach: Fast Proportional Reasoning
Let:
whatA represent the price of a comparable house in City A
whatH represent the price of a comparable house in City H
whatD represent the price of a comparable house in City D

City	Index	Price ($)
J	189	260000
A	153	whatA
H	366	whatH
D	129	whatD

$ (a.) \\[3ex] 189 * whatA = 153 * 260000 \\[3ex] whatA = \dfrac{153 * 260000}{189} \\[5ex] whatA = \dfrac{39780000}{189} \\[5ex] whatA = 210476.1905 \\[3ex] whatA \approx \$210476.19 \\[3ex] (b.) \\[3ex] 189 * whatH = 366 * 260000 \\[3ex] whatH = \dfrac{366 * 260000}{189} \\[5ex] whatH = \dfrac{95160000}{189} \\[5ex] whatH = 503492.0635 \\[3ex] whatH \approx \$503492.06 \\[3ex] (c.) \\[3ex] 189 * whatD = 129 * 260000 \\[3ex] whatD = \dfrac{129 * 260000}{189} \\[5ex] whatD = \dfrac{33540000}{189} \\[5ex] whatD = 177460.3175 \\[3ex] whatD \approx \$177460.32 \\[3ex] $ 2nd Approach: Formula

$ (a.) \\[3ex] price\;(City\;A) = price\;(City\;J) * \dfrac{index\;(City\;A)}{index\;(City\;J)} \\[5ex] = 260000 * \dfrac{153}{189} \\[5ex] = 210476.1905 \\[3ex] \approx \$210,476.19 \\[5ex] (b.) \\[3ex] price\;(City\;H) = price\;(City\;J) * \dfrac{index\;(City\;H)}{index\;(City\;J)} \\[5ex] = 260000 * \dfrac{366}{189} \\[5ex] = 503492.0635 \\[3ex] \approx \$503,492.06 \\[5ex] (c.) \\[3ex] price\;(City\;D) = price\;(City\;J) * \dfrac{index\;(City\;D)}{index\;(City\;J)} \\[5ex] = 260000 * \dfrac{129}{189} \\[5ex] = 177460.3175 \\[3ex] \approx \$177,460.32 $

(10.) Determine the inflation rate from 2006 to 2007.
Assume that all prices have risen at the same rate as the CPI.
Use the CPI table.

$ rate\;\;of\;\;inflation = \dfrac{CPI\;\;of\;\;2007 - CPI\;\;of\;\;2006}{CPI\;\;of\;\;2006} * 100 \\[5ex] = \dfrac{207.342 - 201.6}{201.6} * 100 \\[5ex] = \dfrac{5.742}{201.6} * 100 \\[5ex] = \dfrac{574.2}{201.6} \\[5ex] = 2.848214286 \\[3ex] \approx 2.8\% $

(11.) Total spending on health care in a certain region rose from $864 million in 1978 to $939 billion in 2008.

(a.) By how many percent did health care spending increase?
Round to the nearest percent as needed.

(b.) Determine the overall rate of inflation during that period as measured by the CPI.
Round to the nearest percent as needed.

$ (a.) \\[3ex] initial = \$864\;million = 864,000,000 = 864 * 10^6 = 8.64 * 10^8 \\[3ex] new = \$939\;billion = 939 * 10^9 = 9.39 * 10^2 * 10^9 = 9.39 * 10^{11} \\[3ex] change = new - initial \\[3ex] = 9.39 * 10^{11} - 8.64 * 10^8 \\[3ex] = 10^8(9.39 * 10^3 - 8.64) \\[3ex] = 10^8(9.39 * 1000 - 8.64) \\[3ex] = 10^8(9390 - 8.64) \\[3ex] = 9381.36 * 10^8 \\[3ex] \%\;change \\[3ex] = \dfrac{change}{initial} * 100 \\[5ex] = \dfrac{9381.36 * 10^8}{8.64 * 10^8} * 100 \\[5ex] = 1085.805556 * 100 \\[3ex] = 108580.5556 \\[3ex] \approx 108581\% \\[3ex] (b.) \\[3ex] rate\;\;of\;\;inflation\;\;from\;\;1978\;\;to\;\;2008 \\[3ex] rate\;\;of\;\;inflation = \dfrac{CPI\;\;of\;\;2008 - CPI\;\;of\;\;1978}{CPI\;\;of\;\;1978} * 100 \\[5ex] = \dfrac{215.303 - 65.2}{62.5} * 100 \\[5ex] = \dfrac{150.103}{65.2} * 100 \\[5ex] = \dfrac{15010.3}{65.2} \\[5ex] = 230.2193252 \\[3ex] \approx 230\% $

(12.) What is the purchasing power of $1 in 1980 in terms of 1995 dollars?

$1 in 1980 is worth how much in 1995?
1st Approach: Fast Proportional Reasoning

Year	CPI	Purchasing power
1980	82.4	1
1995	152.4	what

$ 82.4 * what = 152.4 * 1 \\[3ex] what = \dfrac{152.4 * 1}{82.4} \\[5ex] what = \dfrac{152.4}{82.4} \\[5ex] what = 1.849514563 \\[3ex] what \approx \$1.85 \\[3ex] $ 2nd Approach: Formula/Proportional Reasoning
$1 in 1980 is worth how much in 1995?
Even though the reference years for the CPI table are 1982–1984, we shall use 1980 as the reference year because we are given a value ($1 in 1980) to find its worth in 1995.
So, the value is the CPI for 1995 and the reference value is the CPI for 1980.

$ = \dfrac{1995\;\;CPI}{reference\;\;value} \\[5ex] = \dfrac{152.4}{82.4} \\[5ex] = 1.849514563 \\[3ex] \implies \\[3ex] \dfrac{1995\;\;CPI}{1980\;\;CPI} = \dfrac{1.849514563}{1} \\[5ex] $ $1 in 1980 is worth $1.85 in 1995

(13.) Simon needed $1,500 to buy a particular car in 1982.
How much money would have been needed in 2004 to buy the same car?
Assume that all prices have risen at the same rate as the CPI.

In other words, $1500 in 1982 is worth how much in 2004?

1st Approach: Fast Proportional Reasoning

Year	CPI	Cost ($)
1982	96.5	1500
2004	188.9	what

$ 96.5 * what = 188.9 * 1500 \\[3ex] what = \dfrac{188.9 * 1500}{96.5} \\[5ex] what = \dfrac{283350}{96.5} \\[5ex] what = 2936.26943 \\[3ex] what \approx \$2936.27 \\[3ex] $ 2nd Approach: Formula/Proportional Reasoning
Even though the reference years for the CPI table are 1982–1984, we shall use 1982 as the reference year because we are given a value ($1,500 in 1982) to find its worth in 2004.
So, the value is the CPI for 2004 and the reference value is the CPI for 1982.

$ = \dfrac{2004\;\;CPI}{reference\;\;value} \\[5ex] = \dfrac{188.9}{96.5} \\[5ex] = 1.957512953 \\[3ex] \implies \\[3ex] \dfrac{2004\;\;CPI}{1982\;\;CPI} = \dfrac{1.957512953}{1} \\[5ex] $

Proportional Reasoning Method
1982	2004
1	1.957512953
1500	what

$ what * 1 = 1500 * 1.957512953 \\[3ex] what = 2936.26943 \\[3ex] $ $2936.27 would have been needed in 2004 to buy the same car.

(14.) Martha needed $0.23 to buy a particular box of macaroni and cheese in 1976.
How much would it cost to buy the same box of macaroni and cheese in 2008?
Assume that all prices have risen at the same rate as the CPI.

In other words, $0.23 in 1976 is worth how much in 2008?

1st Approach: Fast Proportional Reasoning

Year	CPI	Cost ($)
1976	56.9	0.23
2008	215.303	what

$ 56.9 * what = 0.23 * 215.303 \\[3ex] what = \dfrac{0.23 * 215.303}{56.9} \\[5ex] what = \dfrac{49.51969}{56.9} \\[5ex] what = 0.8702933216 \\[3ex] what \approx \$0.87 \\[3ex] $ 2nd Approach: Formula/Proportional Reasoning
Even though the reference years for the CPI table are 1982–1984, we shall use 1976 as the reference year because we are given a value ($0.23 in 1976) to find its worth in 2008.
So, the value is the CPI for 2008 and the reference value is the CPI for 1976.

$ = \dfrac{2008\;\;CPI}{reference\;\;value} \\[5ex] = \dfrac{215.303}{56.9} \\[5ex] = 3.783884007 \\[3ex] \implies \\[3ex] \dfrac{2008\;\;CPI}{1976\;\;CPI} = \dfrac{3.783884007}{1} \\[5ex] $

Proportional Reasoning Method
1976	2008
1	3.783884007
0.23	what

$ what * 1 = 0.23 * 3.783884007 \\[3ex] what = 0.8702933216 \\[3ex] $ It would cost $0.87 to buy the same box of macaroni and cheese in 2008

(15.) Review the graph shown below.
Adjusted for inflation, during which years during the period shown did the lowest gasoline prices occur?
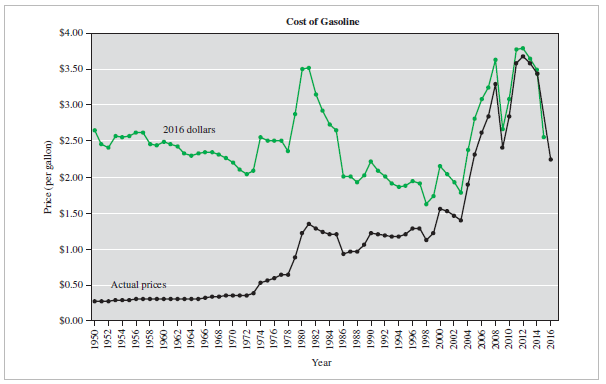
Number 15

The line graph in question is the one with a green color.
The lowest point in the line graph corresponds to the year 1998
Gas was cheapest in 1998–1999, because the graph shows that the price of a gallon of gas in 2016 dollars was at its lowest in that time period.

(16.) Suppose federal government spending for a popular housing program was $1 billion this year and Congress has proposed increasing spending for the program to $1.03 billion for next year.
Assume that the Consumer Price Index is expected to rise by 7% over the next year.
Those who support the program complain that the program is being cut.
Those who oppose the program complain that the program is being increased.
Explain each position.

A. While the housing program gets an increase in actual dollars, when adjusted for inflation, the program gets the same amount of funding.
B. While the housing program gets a decrease in actual dollars, when adjusted for inflation, the program gets more funding.
C. While the housing program gets no change in actual dollars, when adjusted for inflation, the program gets a cut.
D. While the housing program gets an increase in actual dollars, when adjusted for inflation, the program gets a cut.

Compare the funding for the program for each year after taking into account inflation.
D. While the housing program gets an increase in actual dollars, when adjusted for inflation, the program gets a cut.

(19.) The average price of tuition and fees at public 4-year colleges and universities increased from $1710 in 1991 to $7000 in 2006.

(a.) Calculate the relative change in price from 1991 to 2006.
Round to the nearest integer as needed.

(b.) Calculate the overall rate of inflation as measured by the Consumer Price Index.
Round to the nearest integer as needed.

(c.) Compare your answers in (a.) and (b.) and comment.

(d.) If you were a student in any of those colleges/universities and your institution wanted to increase tuition the next year (2007), what would you advise the administration?

$ (a.) \\[3ex] initial = \$1710 \\[3ex] new = \$7000 \\[3ex] change = new - initial \\[3ex] = 7000 - 1710 \\[3ex] = 5290 \\[3ex] \%\;change \\[3ex] = \dfrac{change}{initial} * 100 \\[5ex] = \dfrac{5290}{1710} * 100 \\[5ex] = \dfrac{529000}{1710} \\[5ex] = 309.3567251 \\[3ex] \approx 309\% \\[3ex] (b.) \\[3ex] rate\;\;of\;\;inflation\;\;from\;\;1991\;\;to\;\;2006 \\[3ex] rate\;\;of\;\;inflation = \dfrac{CPI\;\;of\;\;2006 - CPI\;\;of\;\;1991}{CPI\;\;of\;\;1991} * 100 \\[5ex] = \dfrac{201.6 - 136.2}{136.2} * 100 \\[5ex] = \dfrac{65.4}{136.2} * 100 \\[5ex] = \dfrac{6540}{136.2} \\[5ex] = 48.01762115 \\[3ex] \approx 48\% \\[3ex] $ (c.) The increase in tuition and fees in public 4-year colleges is greater than the overall rate of inflation.

(d.) As a student, I would ask the administration not to increase tuition the next year (2007) because the rate of increase from 1991 up to the current year (2006) far exceeds the rate of inflation.
One of the ways of making education accessible to everyone is to ensure that rates of tuition increases are adjusted with inflation rates.

(20.) Suppose Y is the year in which you were born and that $A in year Y is worth $B today.
$C is the face value of $A today.
Is B greater than or less than C?
Use the CPI table to answer the question.

A. B < C because the value of money in general is worth less further back in time than the value today due to deflation.
B. B < C because the cost of an item in general is larger today than the cost of an item further back in time.
C. B > C because the cost of an item in general is smaller today than the cost of an item further back in time.
D. B > C because the value of money in general is worth more further back in time than the value today due to inflation.

As at this year: 2023, the CPI value for 2023 is not yet out.
It will be computed sometime next year: 2024 because it is the annual average of the months.
So, let us assume this year is 2022
Birth year = 1982 = Y
$A in year Y = $1 in year 1982
$B today = $B today (2022)
$C today (2022) = $1 today (2022)
So, the question is:
$1 in 1982 is worth how much in 2022?
$1 in 1982 is $B in 2022
Calculate the value of B

1st Approach: Fast Proportional Reasoning

Year	CPI	Purchasing power
1982	96.5	1
2002	292.655	B

$ 96.5 * B = 292.655 * 1 \\[3ex] B = \dfrac{292.655 * 1}{96.5} \\[5ex] B = \dfrac{292.655}{96.5} \\[5ex] B = 3.032694301 \\[3ex] B \approx \$3.03 \\[3ex] $ 2nd Approach: Formula/Proportional Reasoning
$1 in 1982 is worth how much in 2002?
Even though the reference years for the CPI table are 1982–1984, we shall use 1982 as the reference year because we are given a value ($1 in 1982) to find its worth in 2022.
So, the value is the CPI for 2022 and the reference value is the CPI for 1982.

$ = \dfrac{2002\;\;CPI}{reference\;\;value} \\[5ex] = \dfrac{292.655}{96.5} \\[5ex] = 3.032694301 \\[3ex] \implies \\[3ex] \dfrac{2022\;\;CPI}{1982\;\;CPI} = \dfrac{3.032694301}{1} \\[5ex] $ $1 in 1982 is worth $3.03 in 2022

A = $1.00 in 1982 ⇒ B = $3.03 in 2022
C = $1.00 in 2022
B > C
Based in this context, what one could buy with $3.03 in 2022 could have been bought with $1.00 in 1982
D. B > C because the value of money in general is worth more further back in time than the value today due to inflation.

Top

(21.) The price of gold (end-of-year closing price in dollars per troy ounce) and the CPI index for the given years are given in Table 1.

Table 1
Year	1986	1996	2006	2016
Price	$266	$427	$688	$1026
Average Annual CPI	109.6	156.9	201.6	240.0

(a.) The prices shown in Table 1 are not adjusted for inflation.
Revise the above table to express all prices in terms of 2016 dollars.
Round to the nearest cent as needed.

(b.) If 5 ounces of gold were bought in 1986 and sold in 1996, would there have been a profit (adjusted for inflation in terms of 2016 dollars)?
Explain.

(c.) If 5 ounces of gold were bought in 2006 and sold in 2016, would there have been a profit (adjusted for inflation in terms of 2016 dollars)?
Explain.

(a.)
The question is asking us to express all prices in terms of 2016 dollars.
In other words: $266 in 1986 is how much worth in 2016? Let the worth be price1
$427 in 1996 is how much worth in 2016? Let the worth be price2
$688 in 2006 is how much worth in 2016? Let the worth be price3

1st Approach: Fast Proportional Reasoning Method

Year	Price ($)	CPI
2016 1986 2016 1996 2016 2006	price1 266 price2 427 price3 688	240 109.6 240 156.9 240 201.6

$ \underline{1986} \\[3ex] price1 * 109.6 = 266 * 240 \\[3ex] price1 = \dfrac{63840}{109.6} \\[5ex] price1 = 582.4817518 \\[3ex] price1 \approx \$582.48 \\[3ex] \underline{1996} \\[3ex] price2 * 156.9 = 427 * 240 \\[3ex] price2 = \dfrac{102480}{156.9} \\[5ex] price2 = 653.1548757 \\[3ex] price2 \approx \$653.15 \\[3ex] \underline{2006} \\[3ex] price3 * 201.6 = 688 * 240 \\[3ex] price3 = \dfrac{165120}{201.6} \\[5ex] price3 = 819.047619 \\[3ex] price3 \approx \$819.05 \\[3ex] \underline{2016} \\[3ex] price = \$1026.00 \\[3ex] $ 2nd Approach: Formula

$ \underline{Any\;\;Year} \\[3ex] Price\;\;in\;\;2016\;\;dollars = Price\;\;in\;\;that\;\;year * \dfrac{CPI\;\;for\;\;2016}{CPI\;\;for\;\;that\;\;year} \\[5ex] \underline{1986} \\[3ex] Price\;\;in\;\;2016\;\;dollars \\[3ex] = 266 * \dfrac{240}{109.6} \\[5ex] = \dfrac{63840}{109.6} \\[5ex] = 582.4817518 \\[3ex] \approx \$582.48 \\[3ex] \underline{1996} \\[3ex] Price\;\;in\;\;2016\;\;dollars \\[3ex] = 427 * \dfrac{240}{156.9} \\[5ex] = \dfrac{102480}{156.9} \\[5ex] = 653.1548757 \\[3ex] \approx \$653.15 \\[3ex] \underline{2006} \\[3ex] Price\;\;in\;\;2016\;\;dollars \\[3ex] = 688 * \dfrac{240}{201.6} \\[5ex] = \dfrac{165120}{201.6} \\[5ex] = 819.047619 \\[3ex] \approx \$819.05 \\[3ex] \underline{2016} \\[3ex] Price\;\;in\;\;2016\;\;dollars \\[3ex] = 1026 * \dfrac{240}{240} \\[5ex] = \$1026.00 \\[3ex] $ (b.) In terms of 2016 dollars:
1 troy ounce of gold in 1986 is valued at $582.48
For 5 ounces of gold, this would be valued at 5 * $582.48 = $2912.40
1 troy ounce of gold in 1996 is valued at $653.15
For 5 ounces of gold, this would be valued at 5 * $653.15 = $3265.75
$3265.75 > $2912.40
This implies a profit.
After adjusting for inflation in terms of 2016 dollars, it would cost $2912.40 in 1986.
If it was sold in 1996, it would be valued at $3265.75
Therefore, there have been a profit (of about $3265.75 − $2912.40 = $353.35).

(c.) In terms of 2016 dollars:
1 troy ounce of gold in 2006 is valued at $819.05
For 5 ounces of gold, this would be valued at 5 * $819.05 = $4095.25
1 troy ounce of gold in 2016 is valued at $1026
For 5 ounces of gold, this would be valued at 5 * $1026 = $5130
$5130.00 > $4095.25
This implies a profit.
After adjusting for inflation in terms of 2016 dollars, it would cost $4095.25 in 2006.
If it was sold in 2016, it would be valued at $5130.00
Therefore, there have been a profit (of about $5130.00 − $4095.25 = $1034.75).

(22.) Assume that admission to a movie cost $9.00 in 2008.
What was its price in 1982 dollars?
Assume that all prices have risen at the same rate as the CPI.

In other words, $9.00 in 2008 was worth how much in 1982?

1st Approach: Fast Proportional Reasoning

Year	CPI	Cost ($)
2008	215.303	9
1982	96.5	what

$ 215.303 * what = 9 * 96.5 \\[3ex] what = \dfrac{9 * 96.5}{215.303} \\[5ex] what = \dfrac{868.5}{215.303} \\[5ex] what = 4.03384997 \\[3ex] what \approx \$4.03 \\[3ex] $ 2nd Approach: Formula/Proportional Reasoning
Even though the reference years for the CPI table are 1982–1984, we shall use 2008 as the reference year because we are given a value ($9.00 in 2008) to find its worth in 1982.
So, the value is the CPI for 1982 and the reference value is the CPI for 2008.

$ = \dfrac{1982\;\;CPI}{reference\;\;value} \\[5ex] = \dfrac{96.5}{215.303} \\[5ex] = 0.4482055522 \\[3ex] \implies \\[3ex] \dfrac{1982\;\;CPI}{2008\;\;CPI} = \dfrac{0.4482055522}{1} \\[5ex] $

Proportional Reasoning Method
1982	2008
0.4482055522	1
what	9

$ what * 1 = 9 * 0.4482055522 \\[3ex] what = 4.03384997 \\[3ex] $ Its price in 1982 dollars is $4.03

(23.) The cost of attending a Major League baseball game is summarized by the Fan Cost Index (FCI), which according to its originators is the price of four adult average-price tickets, two small draft beers, four small soft drinks, four regular hot dogs, parking, two programs, and two caps.
The table to the right shows the 2016 FCI for several Major League teams and the Major League average.

Team	FCI
City A City B City C City D City E City F Major League Average	$279.83 $173.08 $375.73 $314.59 $372.24 $137.17 $242.61

(a.) The FCI values are given in dollars. So, is the FCI really an "index"? Explain.

(b.) Consider an index in which the reference value is the 2016 Major League FCI average. That is, set this value equal to 100.
Revise the above table so that all values are expressed in terms of this index.
Type integers or decimals rounded to one decimal place as needed.

(a.) The FCI is not an index.
An index is usually the ratio of two quantities with the same units, which means that it should not have units.

(b.)
1st Approach: Fast Proportional Reasoning Method
Let:
whatA = new FCI for City A
whatB = new FCI for City B
whatC = new FCI for City C
whatD = new FCI for City D
whatE = new FCI for City E
whatF = new FCI for City F

Team	FCI ($)	New FCI ($)
Major League Average	242.61	100
City A	279.83	whatA
City B	173.08	whatB
City C	375.73	whatC
City D	314.59	whatD
City E	372.24	whatE
City F	137.17	whatF

$ \underline{City\;A} \\[3ex] 242.61 * whatA = 279.83 * 100 \\[3ex] whatA = \dfrac{27983}{242.61} \\[5ex] whatA = 115.3414946 \\[3ex] whatA \approx \$115.3 \\[3ex] \underline{City\;B} \\[3ex] 242.61 * whatB = 173.08 * 100 \\[3ex] whatB = \dfrac{17308}{242.61} \\[5ex] whatB = 71.34083509 \\[3ex] whatB \approx \$71.3 \\[3ex] \underline{City\;C} \\[3ex] 242.61 * whatC = 375.73 * 100 \\[3ex] whatC = \dfrac{37573}{242.61} \\[5ex] whatC = 154.8699559 \\[3ex] whatC \approx \$154.9 \\[3ex] \underline{City\;D} \\[3ex] 242.61 * whatD = 314.59 * 100 \\[3ex] whatD = \dfrac{31459}{242.61} \\[5ex] whatD = 129.6690161 \\[3ex] whatD \approx \$129.7 \\[3ex] \underline{City\;E} \\[3ex] 242.61 * whatE = 372.24 * 100 \\[3ex] whatE = \dfrac{37224}{242.61} \\[5ex] whatE = 153.4314332 \\[3ex] whatE \approx \$153.4 \\[3ex] \underline{City\;F} \\[3ex] 242.61 * whatF = 137.17 * 100 \\[3ex] whatF = \dfrac{13717}{242.61} \\[5ex] whatF = 56.53930176 \\[3ex] whatF \approx \$56.5 \\[3ex] $ 2nd Approach: Formula
Reference = Major League Average
Reference Value = FCI = $242.61
Value = New FCI = $100

$ \underline{Any\;\;City} \\[3ex] New\;\;FCI\;\;of\;\;that\;\;City = Value * \dfrac{FCI\;\;of\;\;that\;\;City}{Reference\;\;Value} \\[5ex] \underline{City\;\;A} \\[3ex] New\;\;FCI = 100 * \dfrac{279.83}{242.61} \\[5ex] = \dfrac{27983}{242.61} \\[5ex] = 115.3414946 \\[3ex] \approx \$115.3 \\[3ex] \underline{City\;\;B} \\[3ex] New\;\;FCI = 100 * \dfrac{173.08}{242.61} \\[5ex] = \dfrac{17308}{242.61} \\[5ex] = 71.34083509 \\[3ex] \approx \$71.3 \\[3ex] \underline{City\;\;C} \\[3ex] New\;\;FCI = 100 * \dfrac{375.73}{242.61} \\[5ex] = \dfrac{37573}{242.61} \\[5ex] = 154.8699559 \\[3ex] \approx \$154.9 \\[3ex] \underline{City\;\;D} \\[3ex] New\;\;FCI = 100 * \dfrac{314.59}{242.61} \\[5ex] = \dfrac{31459}{242.61} \\[5ex] = 129.6690161 \\[3ex] \approx \$129.7 \\[3ex] \underline{City\;\;E} \\[3ex] New\;\;FCI = 100 * \dfrac{372.24}{242.61} \\[5ex] = \dfrac{37224}{242.61} \\[5ex] = 153.4314332 \\[3ex] \approx \$153.4 \\[3ex] \underline{City\;\;F} \\[3ex] New\;\;FCI = 100 * \dfrac{137.17}{242.61} \\[5ex] = \dfrac{13717}{242.61} \\[5ex] = 56.53930176 \\[3ex] \approx \$56.5 $

Use the Table of Federal Minimum Wages below and the CPI Table above to answer Questions 25 – 28

Table of Federal Minimum Wages
Year	Actual Dollars	1996 Dollars
1938 1939 1945 1950 1956 1961 1967 1968 1974 1976 1978 1979 1981 1990 1991 1996 1997 2007 2008 2009 2016	$0.25 $0.30 $0.40 $0.75 $1.00 $1.25 $1.40 $1.60 $2.00 $2.30 $2.65 $2.90 $3.35 $3.50 $4.25 $4.75 $5.15 $5.85 $6.55 $7.25 $7.25	$2.75 $3.39 $3.49 $4.88 $5.77 $6.41 $6.58 $7.21 $6.37 $6.34 $6.38 $6.27 $5.78 $4.56 $4.90 $4.75 $5.03 $4.42 $4.77 $5.12 $4.74

(25.) (a.) Use the CPI Table to convert the 1976 minimum wage from actual dollars to 1996 dollars.
(b.) Is the result consistent with the entry in the Table of Federal Minimum Wages?

(a.)
So, here is a paraphrase of the first question:
$2.30 in 1976 is worth how much in 1996?

1st Approach: Fast Proportional Reasoning

Year	CPI	Minimum wage ($)
1976	56.9	2.30
1996	156.9	what

$ 56.9 * what = 156.9 * 2.3 \\[3ex] what = \dfrac{156.9 * 2.3}{56.9} \\[5ex] what = \dfrac{360.87}{56.9} \\[5ex] what = 6.342179262 \\[3ex] what \approx \$6.34 \\[3ex] $ 2nd Approach: Formula/Proportional Reasoning
Table of Federal Minimum Wages
1976 minimum wage = $2.30 (Actual Dollars)

CPI Table
So, here is a paraphrase of the first question:
$2.30 in 1976 is worth how much in 1996?
Even though the reference years for the CPI table are 1982–1984, we shall use 1976 as the reference year because we are given a value ($2.30 in 1976) to find its worth in 1996.
So, the value is the CPI for 1996 and the reference value is the CPI for 1976.

$ = \dfrac{1996\;\;CPI}{reference\;\;value} \\[5ex] = \dfrac{156.9}{56.9} \\[5ex] = 2.757469244 \\[3ex] \implies \\[3ex] \dfrac{1996\;\;CPI}{1976\;\;CPI} = \dfrac{2.757469244}{1} \\[5ex] $

Proportional Reasoning Method
1976	1996
1	2.757469244
2.30	what

$ what * 1 = 2.3 * 27.757469244 \\[3ex] what = 6.342179292 \\[3ex] $ ∴ $2.30 in 1976 is worth $6.34 in 1996

(b.)
Let us verify if this is the same value with the 1996 dollars
Table of Federal Minimum Wages
1976 minimum wage = $2.30 (Actual Dollars) = $6.34 (1996 Dollars)
The results are the same ($6.34 = $6.34).
The result we got from the CPI Table is consistent with the result from the Table of Federal Minimum Dollars

(26.) Explain why the minimum wage for 1996 is the same as 1996 dollars.

A. Since the federal minimum wage in 1996 is in 1996 dollars, the actual dollars are 1996 dollars.

B. The value of 1996 dollars is increasing as the years progress.
The federal minimum wage was scaled to match its growth.

C. The government passed a decree setting the federal minimum wage equal to the value of 1996 dollars.

D. The federal minimum wage in actual dollars and 1996 dollars increase at different rates.
Coincidentally, they happen to be equal in 1996.

A. Since the federal minimum wage in 1996 is in 1996 dollars, the actual dollars are 1996 dollars.

(27.) Use the Table of Federal Minimum Wages
(a.) How high would the minimum wage need to have been in 2007 to match the highest inflation-adjusted value shown in the table (that is, the highest value in 1996 dollars)?
(b.) How does that compare to the actual minimum wage in 2007?

The highest inflation-adjusted value shown in the table (that is, the highest value in 1996 dollars) is $7.21
1st Approach: Fast Proportional Reasoning

Year	Minimum wage ($)	1996 dollars ($)
1996	what	7.21
2007	5.85	4.42

$ what * 4.42 = 5.85 * 7.21 \\[3ex] what = \dfrac{5.85 * 7.21}{4.42} \\[5ex] what = \dfrac{42.1785}{4.42} \\[5ex] what = 9.542647059 \\[3ex] what \approx \$9.54 \\[3ex] $ 2nd Approach: Formula/Proportional Reasoning
The highest inflation-adjusted value shown in the table (that is, the highest value in 1996 dollars) is $7.21
(a.) Because our focus is on 2007, how high the minimum wage in 2007 needs to be in order to match $7.21; first, let us find the index number for the 1996 dollars of 2007

$7.21 in 1996 is our reference value while $4.42 in 2007 is our value.

$ index\;\;number = \dfrac{minimum\;\;wage\;\;of\;\;2007\;\;in\;\;1996\;\;dollars}{highest\;\;minimum\;\;wage\;\;in\;\;1996\;\;dollars} \\[5ex] = \dfrac{4.42}{7.21} \\[5ex] = 0.613037448 \\[3ex] \implies \\[3ex] \dfrac{0.613037448}{1} \\[5ex] $ How much should be the worth of the actual minimum wage in 2007, $5.85 to match the highest minimum wage in 1996 dollars?

Proportional Reasoning Method
2007	1996
0.613037448	1
5.85	what

$ 0.613037448 * what = 5.85 * 1 \\[3ex] what = \dfrac{5.85}{0.613037448} \\[5ex] what = 9.542647059 \\[3ex] $ (b.) In order for the minimum wage in 2007 to match the highest inflation-adjusted value, the minimum wage would need to be $9.54
This is more than the actual minimum wage in 2007

(28.) (a.) Use the average annual consumer price index table to convert the 1981 minimum wage from actual dollars to 1996 dollars.
(b.) Is the result consistent with the entry in the Federal Minimum Wages table?

(a.)
Federal Minimum Wages table: 1981 minimum wage = $3.35
Convert to 1996 dollars using the CPI table
In other words, $3.35 in 1981 is worth how much in 1996?

1st Approach: Fast Proportional Reasoning

Year	CPI	Purchasing power
1981	90.9	3.35
1996	156.9	what

$ 90.9 * what = 3.35 * 156.9 \\[3ex] what = \dfrac{3.35 * 156.9}{90.9} \\[5ex] what = \dfrac{525.615}{90.9} \\[5ex] what = 5.782343234 \\[3ex] what \approx \$5.78 \\[3ex] $ 2nd Approach: Formula/Proportional Reasoning
$3.35 in 1981 is worth how much in 1996?
Even though the reference years for the CPI table are 1982–1984, we shall use 1981 as the reference year because we are given a value ($3.35 in 1981) to find its worth in 1996.
So, the value is the CPI for 1996 and the reference value is the CPI for 1981.

$ price\;\;in\;\;1996 = price\;\;in\;\;1981 * \dfrac{1996\;\;CPI}{reference\;\;value} \\[5ex] = 3.35 * \dfrac{156.9}{90.9} \\[5ex] = \dfrac{525.615}{90.9} \\[5ex] = 5.782343234 \\[3ex] \approx \$5.78 \\[3ex] $ $3.35 in 1981 is worth $5.78 in 1996

(b.)
Federal Minimum Wages table: 1981 minimum wage = $3.35
Federal Minimum Wages table: 1981 minimum wage in 1996 dollars = $5.78
This result is consistent with the entry in the CPI table because the result value is equal to or close to the Federal Minimum Wages table value of $5.78

(29.) The average price of tuition and fees at public 4-year colleges and universities increased from $8,800 in 1992 to $22,000 in 2010.

(a.) Calculate the relative change in price from 1992 to 2010.
Round to the nearest integer as needed.

(b.) Determine the overall rate of inflation as measured by the Consumer Price Index.
Round to the nearest integer as needed.

(c.) Compare your answers in (a.) and (b.) and comment.

(d.) If you were a student in any of those colleges/universities and your institution wanted to increase tuition the next year (2007), what would you advise the administration?

$ (a.) \\[3ex] initial = \$8800 \\[3ex] new = \$22000 \\[3ex] change = new - initial \\[3ex] = 22000 - 8800 \\[3ex] = 13200 \\[3ex] \%\;change \\[3ex] = \dfrac{change}{initial} * 100 \\[5ex] = \dfrac{13200}{8800} * 100 \\[5ex] = \dfrac{1320000}{8800} \\[5ex] = 150\% \\[3ex] (b.) \\[3ex] rate\;\;of\;\;inflation\;\;from\;\;1992\;\;to\;\;2010 \\[3ex] rate\;\;of\;\;inflation = \dfrac{CPI\;\;of\;\;2010 - CPI\;\;of\;\;1992}{CPI\;\;of\;\;1992} * 100 \\[5ex] = \dfrac{218.056 - 140.3}{140.3} * 100 \\[5ex] = \dfrac{77.756}{140.3} * 100 \\[5ex] = \dfrac{7775.6}{140.3} \\[5ex] = 55.4212402 \\[3ex] \approx 55\% \\[3ex] $ (c.) The increase in tuition and fees in public 4-year colleges is greater than the overall rate of inflation.

(d.) As a student, I would ask the administration not to increase tuition the next year (2011) because the rate of increase from 1991 up to the current year (2010) far exceeds the rate of inflation.
One of the ways of making education accessible to everyone is to ensure that rates of tuition increases are adjusted with inflation rates.

(31.) The Heritage Foundation compiles a global economic freedom index, a composite measure of the support that 186 different countries provide for economic and business growth.
Among the factors that comprise the index are business freedom, trade freedom, government spending, and government regulation.
Use the global economic freedom index to answer the questions.

Number 31

(a.) According to the index, what are the only four fully free countries (scores between 80 and 100)?

(b.) Of the fully free countries, which ones have an increasing index?

(c.) Where is country S on the list?
To what do you attribute its (relatively low) ranking?

(a.) According to the index, the only four fully free countries (scores between 80 and 100) are:
Country B: 88.7+
Country E: 90.3+
Country K: 92.2+
Country O: 85.7+

(b.) Of the fully free countries, the ones that have an increasing index are:
Country B: 88.7+
Country E: 90.3+
Country K: 92.2+
Country O: 85.7+

(c.) Country S has a ranking of 9
Its relative low ranking is attributed to Trade Freedom (it's lowest score of 49.5)

(38.) The average price of a domestic airline ticket increased from $251 in 1990 to $414 in 2016.

(a.) Calculate the relative change in price from 1990 to 2016.
Round to the nearest integer as needed.

(b.) Calculate the overall rate of inflation as measured by the Consumer Price Index.
Round to the nearest integer as needed.

(c.) Compare this change to the overall rate of inflation as measured by the Consumer Price Index.

(d.) In "2016 constant dollars," the average domestic airfare for 1990 was $461.
Does this mean that airfares rose more or less than expected with inflation based on the Consumer Price Index? Explain.

$ (a.) \\[3ex] initial = \$251 \\[3ex] new = \$414 \\[3ex] change = new - initial \\[3ex] = 414 - 251 \\[3ex] = 163 \\[3ex] \%\;change \\[3ex] = \dfrac{change}{initial} * 100 \\[5ex] = \dfrac{163}{251} * 100 \\[5ex] = \dfrac{16300}{251} \\[5ex] = 64.94023904 \\[3ex] \approx 65\% \\[5ex] (b.) \\[3ex] rate\;\;of\;\;inflation\;\;from\;\;1990\;\;to\;\;2016 \\[3ex] rate\;\;of\;\;inflation = \dfrac{CPI\;\;of\;\;2016 - CPI\;\;of\;\;1990}{CPI\;\;of\;\;1990} * 100 \\[5ex] = \dfrac{240.007 - 130.7}{130.7} * 100 \\[5ex] = \dfrac{109.307}{130.7} * 100 \\[5ex] = \dfrac{10930.7}{130.7} \\[5ex] = 83.63198164 \\[3ex] \approx 84\% \\[3ex] $ (c.) The change in domestic airline ticket prices was less than the overall rate of inflation.

(d.) Adjusting the domestic airline ticket for inflation:

$ inflation\;\;rate\;\;from\;\;1990\;\;to\;\;2016 = 83.63198164\% \\[3ex] initial = \$251 \\[3ex] 83.63198164\%\;\;of\;\; \$251 \\[3ex] = \dfrac{83.63198164\%}{100} * 251 \\[3ex] = 0.8363198164 * 251 \\[3ex] = 209.9162739\% \\[3ex] new\;\;expected\;\;price = 209.9162739 + 251= \$460.9162739 \\[3ex] \approx \$461 \\[3ex] $ The actual 2016 airfare ($414) is less than it would have been if prices had risen with inflation ($461).

Top