(23.) (I.) Premise: If a body orbits the earth, then it is a satellite.
Premise: The moon orbits the earth.
Conclusion: The moon is a satellite.
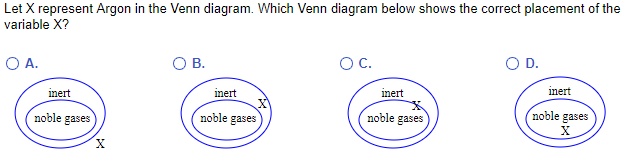
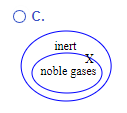
(II.) Let X represent the moon in the Venn diagram.
Which Venn diagram below shows the correct placement of the variable X?

(III.) Is the argument sound?
We already know that the moon is a body.
Hence, let:
$p$: The moon orbits the earth.
$q$: The moon is a satellite.
$ Premise\: 1: p \rightarrow q \\[2ex] Premise\: 2: p \\ \rule{2.5in}{0.5pt} \\ Conclusion\: \therefore q \\[3ex] $ First Method: Valid and Invalid Forms of Arguments
Argument is valid by Modus Ponens (also known as Law of Detachment or Direct Reasoning or Affirming the Hypothesis)
Second Method: Definition
Let us draw a truth table of the premises and the conclusion.
The conclusion is true when both premises are true.
Argument is valid by Definition
Third Method: Formula
Let us draw the truth table for the formula: $[(premise\: 1) \land (premise\: 2)] \rightarrow conclusion$
$[(p \rightarrow q) \land p] \rightarrow q$
The formula is a tautology.
Argument is valid by Formula
(II.) The diagram is:
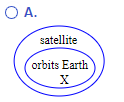
(III.) Because the argument is valid and all it's premises are true, the argument is sound.
Premise: The moon orbits the earth.
Conclusion: The moon is a satellite.
(II.) Let X represent the moon in the Venn diagram.
Which Venn diagram below shows the correct placement of the variable X?

(III.) Is the argument sound?
We already know that the moon is a body.
Hence, let:
$p$: The moon orbits the earth.
$q$: The moon is a satellite.
$ Premise\: 1: p \rightarrow q \\[2ex] Premise\: 2: p \\ \rule{2.5in}{0.5pt} \\ Conclusion\: \therefore q \\[3ex] $ First Method: Valid and Invalid Forms of Arguments
Argument is valid by Modus Ponens (also known as Law of Detachment or Direct Reasoning or Affirming the Hypothesis)
Second Method: Definition
Let us draw a truth table of the premises and the conclusion.
| $p$ | $q$ | $p \rightarrow q$ |
|---|---|---|
| $T\checkmark$ | $T\checkmark$ | $T\checkmark$ |
| $T$ | $F$ | $F$ |
| $F$ | $T$ | $T$ |
| $F$ | $F$ | $T$ |
| Premise 2 | Conclusion | Premise 1 |
The conclusion is true when both premises are true.
Argument is valid by Definition
Third Method: Formula
Let us draw the truth table for the formula: $[(premise\: 1) \land (premise\: 2)] \rightarrow conclusion$
$[(p \rightarrow q) \land p] \rightarrow q$
| $p$ | $q$ | $p \rightarrow q$ | $(p \rightarrow q) \land p$ | $[(p \rightarrow q) \land p] \rightarrow q$ |
|---|---|---|---|---|
| $T$ | $T$ | $T$ | $T$ | $T$ |
| $T$ | $F$ | $F$ | $F$ | $T$ |
| $F$ | $T$ | $T$ | $F$ | $T$ |
| $F$ | $F$ | $T$ | $F$ | $T$ |
The formula is a tautology.
Argument is valid by Formula
(II.) The diagram is:

(III.) Because the argument is valid and all it's premises are true, the argument is sound.
(24.) Consider the following proposition:
"If such procedures are not followed[, then] apes ... act as if they don't understand the problem at hand." — Frans de Waal, Are We Smart Enough to Know How Smart Animals Are?
(I.) What is the logical conclusion if the usual procedures are not followed?
A. The usual procedures were followed.
B. Apes act as if they understand the problem at hand.
C. Apes act as if they don't understand the problem at hand.
D. None of the above is a logical conclusion.
(II.) What is the logical conclusion if apes act as if they understand the problem at hand?
A. Apes act as if they don't understand the problem at hand.
B. Apes act as if they understand the problem at hand.
C. The usual procedures were followed.
D. None of the above is a logical conclusion.
(III.) What is the logical conclusion if the usual procedures are followed?
A. The usual procedures are not followed.
B. Apes act as if they don't understand the problem at hand.
C. Apes act as if they understand the problem at hand.
D. None of the above is a logical conclusion.
(I.) C. Apes act as if they don't understand the problem at hand.
(II.) C. The usual procedures were followed.
(III.) D. None of the above is a logical conclusion.
"If such procedures are not followed[, then] apes ... act as if they don't understand the problem at hand." — Frans de Waal, Are We Smart Enough to Know How Smart Animals Are?
(I.) What is the logical conclusion if the usual procedures are not followed?
A. The usual procedures were followed.
B. Apes act as if they understand the problem at hand.
C. Apes act as if they don't understand the problem at hand.
D. None of the above is a logical conclusion.
(II.) What is the logical conclusion if apes act as if they understand the problem at hand?
A. Apes act as if they don't understand the problem at hand.
B. Apes act as if they understand the problem at hand.
C. The usual procedures were followed.
D. None of the above is a logical conclusion.
(III.) What is the logical conclusion if the usual procedures are followed?
A. The usual procedures are not followed.
B. Apes act as if they don't understand the problem at hand.
C. Apes act as if they understand the problem at hand.
D. None of the above is a logical conclusion.
(I.) C. Apes act as if they don't understand the problem at hand.
(II.) C. The usual procedures were followed.
(III.) D. None of the above is a logical conclusion.