(1.) Explain the reasoning for how you would solve these questions:
(a.) The fact that 1 liter = 1.057 quarts can be expressed as:
(b.) You are given two pieces of information: (1) the volume of a lake in cubic feet and (2) the average depth of the lake in feet. You are asked to find the surface area of the lake in square feet. What should you do?
(c.) You want to know how much total energy is required to operate a 100-watt light bulb. Do you need any more information?
(d.) Which statement best describes a temperature of 110°C?
(e.) The concentration of carbon dioxide in Earth's atmosphere might be stated in which units?
(f.) The guidelines for prescribing a particular drug specify a dose of 300 mg per kilogram of body weight per day.
How should you find how much of the drug should be given to a 30-kg child every 8 hours?
(g.) What does a blood alcohol content (BAC) of 0.08 gm/100 mL mean?
(a.) $\dfrac{1.057\;quart}{1\;liter}$ because multiplying it by any number of liters would convert the number from liters to quarts by causing the units of liters to cancel without changing number because the factor is equal to 1.
Dividing both sides of the given equation by 1 liter, shows that the factor, $\dfrac{1.057\;quart}{1\;liter}$, is equivalent to 1, allowing it to multiply and cancel the units of liter while leaving the units of quarts and without changing the value of the quantity. Therefore, multiplying by the factor only changes the units of what it multiplies.
(b.) Divide the volume by the depth, because this will cancel the depth in the volume and give feet square in the numerator which are the units for surface area.
Dividing the volume by the depth cancels a unit of feet from the numerator, so the numerator will have square feet, and the resulting number will be the area of the surface of the lake since it is the length multiplied by the width of the lake.
(c.) Yes; you need to know how long the light bulb is on because power is the rate at which energy is used, and watts are units of power.
(d.) Hot enough to boil water, since 110°C is above the boiling point of water.
(e.) Parts per million may be used because it gives the number of molecules of carbon dioxide in a million molecules of air.
(f.) 300 mg per kilogram of body weight per day: 30-kg child every 8 hours
Convert day to hours: 1 day = 24 hours
So, this can be reworded as:
300 mg per kilogram of body weight per 24-hours: 30-kg child per 8 hours
$ \underline{Unity\;\;Fraction\;\;Method} \\[3ex] \dfrac{300\;mg}{kg} * \dfrac{1}{24\;hours} * \dfrac{30\;kg} * \dfrac{8\;hours}{1} \\[5ex] $ Multiply 300 mg/kg/day by 30 kg and divide that result by 3, since multiplying will cancel the kg units and dividing by 3 since there are three 8 hour intervals in a day.
(g.) A person with 4 liters of blood has 0.08 * 40 = 3.2 grams of alcohol in his blood because $ \dfrac{0.08g * 40}{100mL * 40} = \dfrac{3.2g}{4L} $
(a.) The fact that 1 liter = 1.057 quarts can be expressed as:
(b.) You are given two pieces of information: (1) the volume of a lake in cubic feet and (2) the average depth of the lake in feet. You are asked to find the surface area of the lake in square feet. What should you do?
(c.) You want to know how much total energy is required to operate a 100-watt light bulb. Do you need any more information?
(d.) Which statement best describes a temperature of 110°C?
(e.) The concentration of carbon dioxide in Earth's atmosphere might be stated in which units?
(f.) The guidelines for prescribing a particular drug specify a dose of 300 mg per kilogram of body weight per day.
How should you find how much of the drug should be given to a 30-kg child every 8 hours?
(g.) What does a blood alcohol content (BAC) of 0.08 gm/100 mL mean?
(a.) $\dfrac{1.057\;quart}{1\;liter}$ because multiplying it by any number of liters would convert the number from liters to quarts by causing the units of liters to cancel without changing number because the factor is equal to 1.
Dividing both sides of the given equation by 1 liter, shows that the factor, $\dfrac{1.057\;quart}{1\;liter}$, is equivalent to 1, allowing it to multiply and cancel the units of liter while leaving the units of quarts and without changing the value of the quantity. Therefore, multiplying by the factor only changes the units of what it multiplies.
(b.) Divide the volume by the depth, because this will cancel the depth in the volume and give feet square in the numerator which are the units for surface area.
Dividing the volume by the depth cancels a unit of feet from the numerator, so the numerator will have square feet, and the resulting number will be the area of the surface of the lake since it is the length multiplied by the width of the lake.
(c.) Yes; you need to know how long the light bulb is on because power is the rate at which energy is used, and watts are units of power.
(d.) Hot enough to boil water, since 110°C is above the boiling point of water.
(e.) Parts per million may be used because it gives the number of molecules of carbon dioxide in a million molecules of air.
(f.) 300 mg per kilogram of body weight per day: 30-kg child every 8 hours
Convert day to hours: 1 day = 24 hours
So, this can be reworded as:
300 mg per kilogram of body weight per 24-hours: 30-kg child per 8 hours
$ \underline{Unity\;\;Fraction\;\;Method} \\[3ex] \dfrac{300\;mg}{kg} * \dfrac{1}{24\;hours} * \dfrac{30\;kg} * \dfrac{8\;hours}{1} \\[5ex] $ Multiply 300 mg/kg/day by 30 kg and divide that result by 3, since multiplying will cancel the kg units and dividing by 3 since there are three 8 hour intervals in a day.
(g.) A person with 4 liters of blood has 0.08 * 40 = 3.2 grams of alcohol in his blood because $ \dfrac{0.08g * 40}{100mL * 40} = \dfrac{3.2g}{4L} $
(2.) ACT The end-on view of a cylindrical milk tank on its support is shown in the figure
below.
The interior radius of the tank's circular end is 4 feet.
The interior length of the tank is 25 feet.
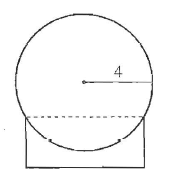
The tank currently holds 5,000 gallons of milk.
Each gallon of milk weighs about 8 pounds.
About how many pounds does this milk weigh?
$ F.\:\: 625 \\[3ex] G.\:\: 4,000 \\[3ex] H.\:\: 4,992 \\[3ex] J.\:\: 5,008 \\[3ex] K.\:\: 40,000 \\[3ex] $
Each gallon means $1$ gallon
$ \underline{First\:\:Method:\:\:Unity\:\:Fraction\:\:Method} \\[3ex] Convert\:\:5000\:gallons\:\:to\:\:pounds \\[3ex] 5000\:gallons * \dfrac{.....pounds}{.....gallons} \\[5ex] 5000\:gallons * \dfrac{8\:pounds}{1\:gallon} \\[5ex] = \dfrac{5000 * 8}{1} \\[5ex] = 40,000\:pounds \\[3ex] \underline{Second\:\:Method:\:\:Proportional\:\:Reasoning\:\:Method} \\[3ex] Let\:\:p\:\:the\:\:converted\:\:unit\:\:in\:\:pounds \\[3ex] $
$ \dfrac{p}{8} = \dfrac{5000}{1} \\[5ex] Cross\:\:Multiply \\[3ex] p * 1 = 8 * 5000 \\[3ex] p = 40,000\:pounds $
The interior radius of the tank's circular end is 4 feet.
The interior length of the tank is 25 feet.

The tank currently holds 5,000 gallons of milk.
Each gallon of milk weighs about 8 pounds.
About how many pounds does this milk weigh?
$ F.\:\: 625 \\[3ex] G.\:\: 4,000 \\[3ex] H.\:\: 4,992 \\[3ex] J.\:\: 5,008 \\[3ex] K.\:\: 40,000 \\[3ex] $
Each gallon means $1$ gallon
$ \underline{First\:\:Method:\:\:Unity\:\:Fraction\:\:Method} \\[3ex] Convert\:\:5000\:gallons\:\:to\:\:pounds \\[3ex] 5000\:gallons * \dfrac{.....pounds}{.....gallons} \\[5ex] 5000\:gallons * \dfrac{8\:pounds}{1\:gallon} \\[5ex] = \dfrac{5000 * 8}{1} \\[5ex] = 40,000\:pounds \\[3ex] \underline{Second\:\:Method:\:\:Proportional\:\:Reasoning\:\:Method} \\[3ex] Let\:\:p\:\:the\:\:converted\:\:unit\:\:in\:\:pounds \\[3ex] $
| gallons | pounds |
|---|---|
| $1$ | $8$ |
| $5000$ | $p$ |
$ \dfrac{p}{8} = \dfrac{5000}{1} \\[5ex] Cross\:\:Multiply \\[3ex] p * 1 = 8 * 5000 \\[3ex] p = 40,000\:pounds $

