Solved Examples: Word Problems on Numbers

For ACT Students
The ACT is a timed exam...60 questions for 60 minutes
This implies that you have to solve each question in one minute.
Some questions will typically take less than a minute a solve.
Some questions will typically take more than a minute to solve.
The goal is to maximize your time. You use the time saved on those questions you solved in less than a minute, to solve the questions that will take more than a minute.
So, you should try to solve each question correctly and timely.
So, it is not just solving a question correctly, but solving it correctly on time.
Please ensure you attempt all ACT questions.
There is no negative penalty for any wrong answer.

For JAMB and CMAT Students
Calculators are not allowed. So, the questions are solved in a way that does not require a calculator.

For WASSCE Students
Any question labeled WASCCE is a question for the WASCCE General Mathematics
Any question labeled WASSCE-FM is a question for the WASSCE Further Mathematics/Elective Mathematics

For NSC Students
For the Questions:
Any space included in a number indicates a comma used to separate digits...separating multiples of three digits from behind.
Any comma included in a number indicates a decimal point.
For the Solutions:
Decimals are used appropriately rather than commas
Commas are used to separate digits appropriately.

Attempt all questions.
Use at least two (two or more) methods whenever applicable.
Show all work.

(1.) ACT Diego purchased a car that had a purchase price of $13,400 which included all other costs and tax.
He paid $400 as a down payment and got a loan for the rest of the purchase price.
Diego paid off the loan by making 48 payments of $300 each.
The total of all his payments, including the down payment, was how much more than the car's purchase price?

$ F.\:\: \$1,000 \\[3ex] G.\:\: \$1,400 \\[3ex] H.\:\: \$13,000 \\[3ex] J.\:\: \$14,400 \\[3ex] K.\:\: \$14,800 \\[3ex] $

Purchase price of car = $\$13,400$

Down payment = $\$400$

$48$ payments @ $\$300$ per payment = $48 * 300 = \$14,400$

Total of all payments he made = $\$400 + \$14,400 = \$14,800$

This is the question:

$\$14,800$ is how much more than $\$13,400$

$14,800 - 13,400 = 1,400$

The total payments made by Diego is $\$1,400$ more than the car's purchase price.

(2.) ACT Ming purchased a car that had a purchase price of $5,400, which included all other costs and tax.
She paid $1,000 as a down payment and got a loan for the rest of the purchase price.
Ming paid off the loan by making 28 payments of $200 each.
The total of all her payments, including the down payment, was how much more than the car's purchase price?

Purchase price of car = $\$5,400$

Down payment = $\$1000$

$28$ payments @ $\$200$ per payment = $28 * 200 = \$5,600$

Total of all payments she made = $\$1000 + \$5,600 = \$6,600$

This is the question:

$\$6,600$ is how much more than $\$5,400$

$6,600 - 5,400 = 1,200$

The total payments made by Ming is $\$1,200$ more than the car's purchase price.

(3.) CSEC In St. Vincent, 3 litres of gasoline cost $EC\$10.40$

(i) Calculate the cost of 5 litres of gasoline in St. Vincent, stating your answer correct to the nearest cent.

(ii) How many litres of gasoline can be bought for $EC\$50.00$ in St. Vincent?
Give your answer correct to the nearest whole number.

$ 10.40 = 10.4 \\[3ex] 50.00 = 50 \\[3ex] $ (i)
Let the cost of $5$ litres of gasoline be $p$

Proportional Reasoning Method
$litres$	$cost(EC\$)$
$3$	$10.4$
$5$	$p$

$ \dfrac{p}{5} = \dfrac{10.4}{3} \\[5ex] Multiply\:\:both\:\:sides\:\:by\:\:5 \\[3ex] 5 * \dfrac{p}{5} = 5 * \dfrac{10.4}{3} \\[5ex] p = \dfrac{5 * 10.4}{3} \\[5ex] p = \dfrac{52}{3} \\[5ex] p = 17.3333333 \\[3ex] p \approx EC\$17.33 \\[3ex] $ The cost of $5$ litres of gasoline is $EC\$17.33$

(ii)
Let the volume of gasoline that can be bought for $EC\$50.00$ be $k$

Proportional Reasoning Method
$litres$	$cost(EC\$)$
$3$	$10.4$
$k$	$50$

$ \dfrac{k}{3} = \dfrac{50}{10.4} \\[5ex] Multiply\:\:both\:\:sides\:\:by\:\:3 \\[3ex] 3 * \dfrac{k}{3} = 3 * \dfrac{50}{10.4} \\[5ex] k = \dfrac{3 * 50}{10.4} \\[5ex] k = \dfrac{150}{10.4} \\[5ex] k = 14.4230769 \\[3ex] k \approx 14\:\:litres \\[3ex] $ About $14$ litres of gasoline can be bought with $EC\$50.00$

(4.) ACT The length of a rectangle is $12$ feet.

The width of the rectangle is $\dfrac{1}{2}$ the length.

What is the perimeter of the rectangle, in feet?

$ F.\:\: 18 \\[3ex] G.\:\: 24 \\[3ex] H.\:\: 30 \\[3ex] J.\:\: 36 \\[3ex] K.\:\: 72 \\[3ex] $

$ Length = 12 \\[3ex] Width = \dfrac{1}{2} * 12 = 1 * 6 = 6 \\[5ex] Perimeter = 2 * Length + 2 * Width \\[3ex] = 2(12) + 2(6) \\[3ex] = 24 + 12 \\[3ex] = 36\:\:feet $

(5.) ACT When Tyrone fell asleep one night, the temperature was $24^\circ F$.
When Tyrone awoke the next morning, the temperature was $-12^\circ F$.
Letting $+$ denote a rise in temperature and $-$ denote a drop in temperature, what was the change in temperature from the time Tyrone fell asleep until the time he awoke?

$ F.\:\: -36^\circ F \\[3ex] G.\:\: -12^\circ F \\[3ex] H.\:\: +6^\circ F \\[3ex] J.\:\: +12^\circ F \\[3ex] K.\:\: +36^\circ F \\[3ex] $

$ Initial\:\:temperature = 24^\circ F \\[3ex] Final\:\:temperature = -12^\circ F \\[3ex] Change\:\:in\:\:temperature = Final\:\:temperature - Initial\:\:temperature \\[3ex] = -12 - 24 \\[3ex] = -36^\circ F $

(6.) ACT Discount tickets to a basketball tournament sell for $4.00 each.
Enrico spent $60.00 on discount tickets, $37.50 less than if he had bought the tickets at the regular price.
What was the regular ticket price?

$ F.\:\: \$2.50 \\[3ex] G.\:\: \$6.40 \\[3ex] H.\:\: \$6.50 \\[3ex] J.\:\: \$7.50 \\[3ex] K.\:\: \$11.00 \\[3ex] $

Notice the wording of the question: regular ticket price.
This means that they want us to find the price of one regular ticket, NOT the price of all the regular tickets

First: Let us find the number of tickets that he bought by dividing the price of all the discount tickets by the price of one discount ticket

Second: We find the price of all the regular tickets
The price of all discount tickets is the price of all regular tickets minus $37.50$
This implies that the price of all the regular tickets is the price of all the discount tickets plus $37.50$

Third: We find the price of a regular ticket by dividing the price of all the regular tickets by the number of tickets

$ \underline{First} \\[3ex] Price\:\:of\:\:all\:\:discount\:\:tickets = 60.00 \\[3ex] Price\:\:of\:\:a\:\:discount\:\:ticket = 4.00 \\[3ex] Number\:\:of\:\:tickets = \dfrac{60}{4} = 15 \\[5ex] \underline{Second} \\[3ex] Price\:\:of\:\:all\:\:regular\:\:tickets = 60 + 37.50 = 97.50 \\[3ex] \underline{Third} \\[3ex] Price\:\:of\:\:a\:\:regular\:\:ticket = \dfrac{97.50}{15} = 6.50 \\[3ex] $ The price of a regular ticket is $\$6.50$

(7.) ACT Xuan sold $9$ used books for $9.80 each.
With the money from these sales, she bought $4$ new books and had $37.80 left over.
What was the average amount Xuan paid for each new book?

$ A.\:\: \$5.60 \\[3ex] B.\:\: \$9.45 \\[3ex] C.\:\: \$10.08 \\[3ex] D.\:\: \$22.05 \\[3ex] $

$ \underline{Sold} \\[3ex] Selling\:\:price = 9\:\:used\:\:books\:\:@\:\:\$9.80\:\:each \\[3ex] = 9 * 9.8 \\[3ex] = \$88.2 \\[3ex] \underline{Bought} \\[3ex] 4\:\:new\:\:books\:\:with\:\:\$37.80\:\:remaining \\[3ex] Cost\:\:of\:\:the\:\:4\:\:new\:\:books = 88.2 - 37.80 \\[3ex] = \$50.4 \\[3ex] Average\:\:cost\:\:of\:\:each\:\:new\:\:book \\[3ex] = \dfrac{50.4}{4} \\[5ex] = \$12.6 \\[3ex] $ The average cost of each new book is $\$12.60$

(8.) ACT Given today is Tuesday, what day of the week was it $200$ days ago?

$ A.\:\: Monday \\[3ex] B.\:\: Tuesday \\[3ex] C.\:\: Wednesday \\[3ex] D.\:\: Friday \\[3ex] E.\:\: Saturday \\[3ex] $

Let us look at this first:
If today is Tuesday,
Yesterday, (a day ago); it was Monday
$2$ days ago, it was Sunday
$3$ days ago, it was Saturday
$4$ days ago, it was Friday
$5$ days ago, it was Thursday
$6$ days ago, it was Wednesday
$7$ days ago (a week ago), it was Tuesday
$7$ days make a week.
$14$ days ago (2 weeks ago), it was Tuesday
So, let us find how many weeks and days there are in $200$ days.

$ 200\:\: days \\[3ex] 200 \div 7 = 28 + remainder \\[3ex] We\:\: have\:\: 28\:\: weeks \\[3ex] 28 * 7 = 196 \\[3ex] 200 - 196 = 4\:\: days \\[3ex] $ There are $28$ weeks and $4$ days in $200$ days
$196$ days ago (28 weeks ago), it was Tuesday
$197$ days ago, it was Monday
$198$ days ago, it was Sunday
$199$ days ago, it was Saturday
$200$ days ago, it was Friday

(9.) CSEC The table below shows a shopping bill prepared for Mrs Rowe.
The prices of some items are missing.

Shopping Bill
Item	Unit Cost Price	Total Cost Price
$3$ kg sugar	$X$	$\$10.80$
$4$ kg rice	$Y$	$Z$
$2$ kg flour	$\$1.60$	$\$3.20$

(i) Calculate the value of $X$, the cost of $1\:kg$ of sugar.

(ii) If the cost price of $1\:kg$ of rice is $80$ cents MORE than for $1\:kg$ of flour, calculate the values of $Y$ and $Z$.

(iii) A tax of $10\%$ of the total cost price of the three items is added to Mrs Rowe's bill.
What is Mrs Rowe's TOTAL bill including the tax?

(i)
Unit cost implies the price for $1$ unit

Proportional Reasoning Method
Item (kg)	Cost ($\$$)
$3$	$10.80$
$1$	$X$

$ \dfrac{X}{1} = \dfrac{10.80}{3} \\[5ex] X = 3.6 \\[3ex] X = \$3.60 \\[3ex] $ The cost of $1$ kg of sugar is $\$3.60$

(ii)
The cost price for $1$ kg of rice is Y, and it is $80$ cents more than for $1$ kg of flour
The unit cost (the cost for $1$ kg) of flour is $\$1.60$
This means that $Y$ is $80$ cents more than $\$1.60$

$ 80\:\:cents = \dfrac{80}{100} = 0.8 \\[5ex] Y = 0.8 + 1.6 \\[3ex] Y = 2.4 \\[3ex] Y = \$2.40 \\[3ex] $ The cost of $1$ kg of rice is $\$2.40$

$ Z = cost\:\:of\:\:4\:\:kg\:\:of\:\:rice \\[3ex] Z = 4 * 2.40 \\[3ex] Z = 9.6 \\[3ex] Z = \$9.60 \\[3ex] $ Therefore, the cost of $4$ kg of rice will be $\$9.60$

$ (iii) \\[3ex] Total\:\:cost\:\:price\:\:of\:\:all\:\:three\:\:items \\[3ex] = 10.80 + Z + 3.20 \\[3ex] = 10.80 + 9.60 + 3.20 \\[3ex] = 23.6 \\[3ex] 10\%\:\:tax\:\:of\:\:23.6 \\[3ex] = \dfrac{10}{100} * 23.6 \\[5ex] = 0.1 * 23.6 \\[3ex] = 2.36 \\[3ex] Total\:\:bill \\[3ex] = 23.6 + 2.36 \\[3ex] = 25.96 \\[3ex] = \$25.96 $

(10.) ACT Mr. Dietz is a teacher whose salary is $\$22,570$ for this school year, which has $185$ days.
In Mr. Dietz's school district, substitute teachers are paid $\$80$ per day.
If Mr. Dietz takes a day off without pay and a substitute teacher is paid to teach Mr. Dietz's classes, how much less does the school district pay in salary by paying a substitute teacher instead of paying Mr. Dietz for that day?

$ A.\:\: \$42 \\[3ex] B.\:\: \$80 \\[3ex] C.\:\: \$97 \\[3ex] D.\:\: \$105 \\[3ex] E.\:\: \$122 \\[3ex] $

$ \underline{Mr.\:\:Dietz} \\[3ex] School\:\:Year\:\:salary = \$22,570 \\[3ex] School\:\:Days\:\: = 185\:\:days \\[3ex] Average\:\:daily\:\:pay = \dfrac{22570}{185} = \$122 \\[5ex] \underline{Substitute\:\:teacher} \\[3ex] Daily\:\:pay = \$80 \\[3ex] For\:\:one\:\:day: \\[3ex] Difference = 122 - 80 = 42 \\[3ex] $ The school district saved $\$42$ by paying the substitute teacher on the day Mr. Dietz was absent.

(11.) ACT A construction company builds $3$ different models of houses (A, B, and C).
They order all the bathtubs, shower stalls, and sinks for the houses from a certain manufacturer.
Each model of house contains different numbers of these bathroom fixtures.
The tables below give the number of each kind of these fixtures required for each model and the cost to the company, in dollars, or each type of fixture.

Fixture	Model
Fixture	A	B	C
Bathtubs Shower stalls Sinks	$1$ $0$ $1$	$1$ $1$ $2$	$2$ $1$ $4$

Fixture	Cost
Bathtubs Shower stalls Sinks	$\$250$ $\$150$ $\$120$

The company plans to build $3$ A's, $4$ B's, and $6$ C's.
What will be the cost to the company of exactly enough of these bathroom fixtures to put the required number in all of these houses?

$ F.\:\: \$1,940 \\[3ex] G.\:\: \$2,070 \\[3ex] H.\:\: \$8,940 \\[3ex] J.\:\: \$9,180 \\[3ex] K.\:\: \$10,450 \\[3ex] $

Model A requires $1$ bathtub, no shower stall, and $1$ sink

Model B requires $1$ bathtub, $1$ shower stall, and $2$ sinks

Model C requires $2$ bathtubs, $1$ shower stall, and $4$ sinks

A bathtub costs $\$250$

A shower stall costs $\$150$

A sink costs $\$120$

$ Cost\:\:of\:\:Model\:\:A \\[3ex] = 1(250) + 0(150) + 1(120) \\[3ex] = 250 + 0 + 120 \\[3ex] = \$370 \\[3ex] Cost\:\:of\:\:3\:\:A's \\[3ex] = 3(370) \\[3ex] = \$1110 \\[3ex] Cost\:\:of\:\:Model\:\:B \\[3ex] = 1(250) + 1(150) + 2(120) \\[3ex] = 250 + 150 + 240 \\[3ex] = \$640 \\[3ex] Cost\:\:of\:\:4\:\:B's \\[3ex] = 4(640) \\[3ex] = \$2560 \\[3ex] Cost\:\:of\:\:Model\:\:C \\[3ex] = 2(250) + 1(150) + 4(120) \\[3ex] = 500 + 150 + 480 \\[3ex] = \$1130 \\[3ex] Cost\:\:of\:\:6\:\:C's \\[3ex] = 6(1130) \\[3ex] = \$6780 \\[3ex] Total\:\:Cost \\[3ex] = 1110 + 2560 + 6780 \\[3ex] = \$10,450 $

(12.) CSEC The diagram below, not drawn to scale, shows two jars of peanut butter of the same brand.

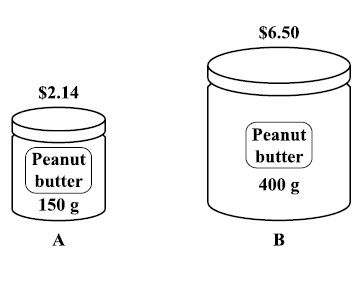
Which of the jars shown above is the BETTER buy?
Show ALL working to support your answer.

We can do this question in at least two ways...Without a Calculator and With a Calculator.
Use any method you prefer.

First Method: Proportional Reasoning Method
This method uses a calculator.

To determine the better buy, we need to calculate the cost of a unit gram (cost of 1 gram) of peanut butter for each jar.
The jar that has the least cost for a unit gram of peanut butter is the better buy.
Let the unit cost of peanut butter in Jar A = $A$
Let the unit cost of peanut butter in Jar B = $B$

Proportional Reasoning Method (Jar A)
$Amount (g)$	$Cost (\$)$
$150$	$2.14$
$1$	$A$

$ \dfrac{A}{1} = \dfrac{2.14}{150} \\[5ex] A = 0.0142666667 \\[3ex] A \approx \$0.01 \\[3ex] $

Proportional Reasoning Method (Jar B)
$Amount (g)$	$Cost (\$)$
$400$	$6.50$
$1$	$B$

$ \dfrac{B}{1} = \dfrac{6.5}{400} \\[5ex] B = 0.01625 \\[3ex] B \approx \$0.02 \\[3ex] $ Jar $A$ costs about a cent for a unit gram of peanut butter
Jar $B$ costs about two cents for a unit gram of peanut butter
Jar $A$ is the better buy because it costs less for a unit gram of peanut butter.

Second Method: Quantitative Reasoning Method
This method does not need a calculator.

$ \underline{Jar\:A} \\[3ex] 150\:g\:\:for\:\:\$2.14 \\[3ex] 2(150)\:\:g\:\:for\:\:2(2.14) \rightarrow 300\:g\:\:for\:\:\$4.28 \\[3ex] 3(150)\:\:g\:\:for\:\:3(2.14) \rightarrow 450\:g\:\:for\:\:\$6.42 \\[3ex] 3\:\:jars\:\:of\:\:A = 450g\:\:for\:\:\$6.42 \\[3ex] \underline{Jar\:\:B} \\[3ex] 400\:g\:\:for\:\:\$6.50 \\[3ex] Compare: \\[3ex] 450\:g\:\:for\:\:\$6.42\:\:versus\:\:400\:g\:\:for\:\:\$6.50 \\[3ex] 450\:g\:\:for\:\:\$6.42\:\:much\:\:better...get\:\:more\:\:for\:\:less \\[3ex] \therefore Jar\:A\:\:is\:\:the\:\:better\:\:buy $

(13.) ACT The total cost of renting a car is $\$35.00$ for each day the car is rented plus $42.5¢$ for each mile the car is driven.
What is the total cost of renting the car for $6$ days and driving $350$ miles?
(Note: No sales tax is involved.)

$ A.\:\: \$154.75 \\[3ex] B.\:\: \$224.88 \\[3ex] C.\:\: \$358.75 \\[3ex] D.\:\: \$420.00 \\[3ex] E.\:\: \$1,697.50 \\[3ex] $

The answer options are in dollars.

Therefore, we need to convert the $42.5$ cents to dollars.

It is required that we work in the same unit.

$ \underline{Cost\:\:of\:\:renting} \\[3ex] 6\:\:days\:\:@\:\:\$35.00\:\:per\:\:day = 6(35) = \$210 \\[3ex] \underline{Cost\:\:of\:\:driving} \\[3ex] 100¢ = \$1 \\[3ex] 42.5¢ = \dfrac{42.5}{100} = \$0.425 \\[3ex] 350\:\:miles\:\:@\:\:\$0.425\:\:per\:\:mile = 350(0.425) = \$148.75 \\[3ex] \underline{Total\:\:Cost} \\[3ex] Total\:\:Cost = \$210 + \$148.75 = \$358.75 \\[3ex] $ The total cost of renting the car for $6$ days and driving $350$ miles is $\$358.75$

(14.) ACT Taho earns his regular pay of $\$11$ per hour for up to $40$ hours of work per week.
For each hour over $40$ hours of work per week, Taho earns $1\dfrac{1}{2}$ times his regular pay.
How much does Taho earn in a week in which he works $50$ hours?

$ F.\:\: \$550 \\[3ex] G.\:\: \$605 \\[3ex] H.\:\: \$625 \\[3ex] J.\:\: \$750 \\[3ex] K.\:\: \$825 \\[3ex] $

$ Work\:\:hours = 50 \\[3ex] Regular\:\:work\:\:hours = 40 \\[3ex] Overtime\:\:work\:\:hours = 50 - 40 = 10 \\[3ex] \underline{Regular\:\:Work\:\:Hours} \\[3ex] Regular\:\:pay = \$11\:\:per\:\:hour \\[3ex] 40\:hours\:\:@\:\:\$11\:\:per\:\:hour = 40(11) = \$440 \\[3ex] \underline{Overtime\:\:Work\:\:Hours} \\[3ex] 1\dfrac{1}{2} = \dfrac{2 * 1 + 1}{2} = \dfrac{2 + 1}{2} = \dfrac{3}{2} = 1.5 \\[5ex] Overtime\:\:pay = 1.5(11) = \$16.5\:\:per\:\:hour \\[3ex] 10\:hours\:\:@\:\:\$16.5\:\:per\:\:hour = 10(16.5) = \$165 \\[3ex] \underline{Total\:\:Pay} \\[3ex] Total\:\:pay\:\:for\:\:50\:\:hours\:\:of\:\:work \\[3ex] = \$440 + \$165 = \$605 $

ACT Use the following information to answer questions 15 – 17
A large theater complex surveyed 5,000 adults.
The results of the survey are shown in the tables below.

Age groups	Number
21 – 30 31 – 40 41 – 50 51 or older	2,750 1,225 625 400

Moviegoer category	Number
Very often Often Sometimes Rarely	830 1,650 2,320 200

Tickets are $9.50 for all regular showings and $7.00 for matinees.

(15.) ACT Based on the survey results, what was the average number of moviegoers for each of the 4 categories?

$ A.\:\: 610 \\[3ex] B.\:\: 1,060 \\[3ex] C.\:\: 1,240 \\[3ex] D.\:\: 1,250 \\[3ex] E.\:\: 1,985 \\[3ex] $

$ Average = Mean = \bar{x} \\[3ex] \bar{x} = \dfrac{\Sigma x}{n} \\[5ex] \Sigma x = 830 + 1650 + 2320 + 200 = 5000 \\[3ex] n = 4 \\[3ex] \bar{x} = \dfrac{5000}{4} \\[5ex] \bar{x} = 1250 \\[3ex] $ The average number of moviegoers for each of the $4$ categories is $1250$ moviegoers

(16.) ACT Suppose all the adults surveyed happened to attend 1 movie each in one particular week.
The total amount spent on tickets by those surveyed in that week was $\$44,000.00$
How many adults attended matinees that week?

$ F.\:\: 500 \\[3ex] G.\:\: 1,400 \\[3ex] H.\:\: 2,500 \\[3ex] J.\:\: 3,600 \\[3ex] K.\:\: 4,500 \\[3ex] $

$ Let\:\:the: \\[3ex] Number\:\:of\:\:adults\:\:that\:\:attended\:\:matinees = m \\[3ex] Number\:\:of\:\:adults\:\:that\:\:attended\:\:regular\:\:showings = r \\[3ex] Adults:\:\: m + r = 5000...eqn.(1) \\[3ex] Cost:\:\: 7m + 9.5r = 44000...eqn.(2) \\[3ex] To\:\:find\:\:m, \:\:eliminate\:\: r \\[3ex] 9.5 * eqn.(1) \implies 9.5m + 9.5r = 47500...eqn.(3) \\[3ex] eqn.(3) - eqn.(2) \implies \\[3ex] (9.5m - 7m) + (9.5r - 9.5r) = 47500 - 44000 \\[3ex] 2.5m = 3500 \\[3ex] m = \dfrac{3500}{2.5} \\[5ex] m = 1400 \\[3ex] $ $1400$ adults attended matinees that week.

(17.) ACT One of the following circle graphs represents the proportion by age group of the adults surveyed. Which one?

Age groups	Number	Percentage
$21 - 30$	$2,750$	$ \dfrac{2750}{5000} * 100 = 0.55 * 100 = 55\% $
$31 - 40$	$1,225$	$ \dfrac{1225}{5000} * 100 = 0.245 * 100 = 24.5\% $
$41 - 50$	$625$	$ \dfrac{625}{5000} * 100 = 0.125 * 100 = 12.5\% $
$51$ or older	$400$	$ \dfrac{400}{5000} * 100 = 0.08 * 100 = 8\% $

The correct option is $A$

(18.) ACT Pablo recorded the noon temperature, in degrees Celsius, on $4$ consecutuve days as part of a science project.
On the 1st day, the noon temperature was -4°C.
On the 4th day, the noon temperature was 12°C.
What was the change in the noon temperature from the 1st day to the 4th day?

$ F.\:\: -16^\circ C \\[3ex] G.\:\: -4^\circ C \\[3ex] H.\:\: 4^\circ C \\[3ex] J.\:\: 8^\circ C \\[3ex] K.\:\: 16^\circ C \\[3ex] $

$ Initial\:\:temperature = temperature\:\:on\:\:the\:\:1st\:\:day = -4^\circ C \\[3ex] Final\:\:temperature = temperature\:\:on\:\:the\:\:4th\:\:day = 12^\circ C \\[3ex] Change\:\:in\:\:temperature \\[3ex] = Final\:\:temperature - Initial\:\:temperature \\[3ex] = 12 - (-4) \\[3ex] = 12 + 4 \\[3ex] = 16^\circ C $

ACT Use the following information to answer questions $19 - 21$
Kyla purchased $25$ pieces of candy from Laszko's Candy Shop.
Her purchase consists of $7$ lollipops, $4$ candy bars, $10$ licorice sticks, and $4$ gumballs.
The unit price of each candy item is shown in the table below.
Kyla's purchase, without sales tax, totaled $\$10.30$.
Laszko's charges an $8\%$ sales tax on each purchase, which is calculated by multiplying the purchase total by $0.08$ and rounding to the nearest $\$0.01$.

Candy Item	Unit price
Lollipop Candy bar Licorice stick Gumball	$\$0.90$ $\$0.60$ $\$0.10$ $\$0.15$

(19.) ACT Kyla gave the shop clerk $\$15.00$.
How much change should Kyla have received?

$ A.\:\: \$3.88 \\[3ex] B.\:\: \$4.35 \\[3ex] C.\:\: \$4.62 \\[3ex] D.\:\: \$4.70 \\[3ex] E.\:\: \$5.08 \\[3ex] $

$ Kyla's\:\:purchase\:\:without\:\:sales\:\:tax = \$10.30 \\[3ex] 8\%\:\:sales\:\:tax = 0.08(10.30) = 0.824 \\[3ex] Checkout\:\:price = 10.30 + 0.824 = 11.124 \approx \$11.12 \\[3ex] Gave\:\: \$15.00 \\[3ex] Change = 15.00 - 11.12 = \$3.88 $

(20.) ACT Without sales tax, what was the average price Kyla paid per piece of candy, to the nearest $\$0.01?$

$ F.\:\: \$0.21 \\[3ex] G.\:\: \$0.25 \\[3ex] H.\:\: \$0.32 \\[3ex] J.\:\: \$0.41 \\[3ex] K.\:\: \$0.44 \\[3ex] $

$ Average\:\:price = \dfrac{\$10.30}{25} \\[5ex] = \$0.412 \:\:per\:\: candy \\[3ex] \approx \$0.41 \:\:per\:\: candy $

Top

(21.) ACT Kyla offers to sell $2$ of the $25$ pieces of candy to her brother Virgil.
She lets Virgil have a choice of $2$ pieces of the same candy item or $1$ piece each of $2$ different candy items.
Kyla will have Virgil pay the same total cost for the $2$ pieces that he would pay for the $2$ pieces at Laszko's.
How many different total costs (in dollars) are possible for Virgil's choice of $2$ pieces?

$ A.\:\: 8 \\[3ex] B.\:\: 10 \\[3ex] C.\:\: 12 \\[3ex] D.\:\: 14 \\[3ex] E.\:\: 16 \\[3ex] $

We can do this in at least two ways.
The first method involves Quantitative Literacy
The second method is Combinatorics.
Use any method you prefer.

$ \underline{First\:\:Method: - Quantitative\:\:Reasoning} \\[3ex] Combinations\:\:are \\[3ex] 1\:Lollipop \:\:and\:\: 1\:Candy\:\:bar \\[3ex] 1\:Lollipop \:\:and\:\: 1\:Licorice\:\:stick \\[3ex] 1\:Lollipop \:\:and\:\: 1\:Gumball \\[3ex] 1\:Candy\:\:bar \:\:and\:\: 1\:Licorice\:\:stick \\[3ex] 1\:Candy\:\:bar \:\:and\:\: 1\:Gumball \\[3ex] 1\:Licorice\:\:stick \:\:and\:\: 1\:Gumball \\[3ex] 2\:Lollipops \\[3ex] 2\:Candy\:\:bars \\[3ex] 2\:Licorice\:\:sticks \\[3ex] 2\:Gumballs \\[3ex] = 10\:\:combinations $

(22.) ACT Marietta purchased a car that had a purchase price of $10,400, which included all other costs and tax.
She paid $2,000 as a down payment and got a loan for the rest of the purchase price.
Marietta paid off the loan by making 48 payments of $225 each.
The total of all her payments, including the down payment, was how much more than the car's purchase price?

$ A.\:\: \$400 \\[3ex] B.\:\: \$2,400 \\[3ex] C.\:\: \$8,400 \\[3ex] D.\:\: \$10,800 \\[3ex] E.\:\: \$12,800 \\[3ex] $

$ Purchase price of car = $\$10,400$

Down payment = $\$2000$

$48$ payments @ $\$225$ per payment = $48 * 225 = \$10,800$

Total of all payments she made = $\$2000 + \$10,800 = \$12,800$

This is the question:

$\$12,800$ is how much more than $\$10,400$

$12,800 - 10,400 = 2,400$

The total payments made by Marietta is $\$2,400$ more than the car's purchase price. $

ACT Use the following information to answer questions $23 - 24$
The table below gives the price per gallon of unleaded gasoline at Gus's Gas Station on January $1$ for $5$ consecutive years in the $1990s$.
At Gus's, a customer can purchase a car wash for $\$4.00$.

Year	Price
$1$ $2$ $3$ $4$ $5$	$\$1.34$ $\$1.41$ $\$1.41$ $\$1.25$ $\$1.36$

(23.) ACT What is the mean price per gallon, to the nearest $\$0.01$, on January $1$ for the $5$ years listed in the table?

$ F.\:\: \$3.88 \\[3ex] G.\:\: \$4.35 \\[3ex] H.\:\: \$4.62 \\[3ex] J.\:\: \$4.70 \\[3ex] K.\:\: \$5.08 \\[3ex] $

$ Mean = \dfrac{1.34 + 1.41 + 1.41 + 1.25 + 1.36}{5} \\[5ex] = \dfrac{6.77}{5} \\[5ex] = 1.354 \\[3ex] \approx \$1.35 $

(24.) ACT On January $1$ of Year $5$, Anamosa bought gas and a car wash at Gus's.
She put $11.38$ gallons of gas in her car and $1.85$ gallons of gas in a container for her snowblower.
To the nearest $\$0.01$, how much did Anamosa pay for the gas for her car and snowblower, and a car wash?

$ F.\:\: \$15.48 \\[3ex] G.\:\: \$17.23 \\[3ex] H.\:\: \$17.99 \\[3ex] J.\:\: \$19.48 \\[3ex] K.\:\: \$21.99 \\[3ex] $

$ \underline{January\:\:1\:\:of\:\:Year\:\:5} \\[3ex] Total\:\:gallons\:\:of\:\:gas\:\:purchased = 11.38 + 1.85 = 13.23 \\[3ex] 13.23\:\:gallons\:\:@\:\:\$1.36\:\:per\:\:gallon = 13.23(1.36) = \$17.9928 \\[3ex] Car\:\:wash = \$4.00 \\[3ex] Total\:\:cost = \$17.9928 + \$4.00 = \$21.9928 \\[3ex] \approx \$21.99\:\:to\:\:the\:\:nearest\:\:\$0.01 $

(25.) CSEC The table below shows the number of tickets sold for a bus tour.
Some items in the table are missing.

Tickets Sold for Bus Tour
Category	Number of Tickets Sold	Cost per Ticket in $\$$	Total Cost in $\$$
Juvenile	$5$	$P$	$130.50$
Youth	$14$	$44.35$	$Q$
Adult	$R$		$2483.60$

(i) Calculate the value of $P$
(ii) Calculate the value of $Q$
(iii) An adult ticket is TWICE the cost of a youth ticket. Calculate the value of $R$
(iv) The bus company pays taxes of $15\%$ on each ticket sold. Calculate the taxes paid by the bus company.

$ Number\;\;of\;\;tickets\;\;sold * Cost\;\;per\;\;ticket = Total\;\;cost \\[3ex] (i) \\[3ex] \underline{Juvenile} \\[3ex] 5 * P = 130.50 \\[3ex] P = \dfrac{130.5}{5} \\[5ex] P = \$26.10 \\[3ex] (ii) \\[3ex] \underline{Youth} \\[3ex] 14 * 44.35 = Q \\[3ex] 620.9 = Q \\[3ex] Q = \$620.90 \\[3ex] (iii) \\[3ex] \underline{Adult} \\[3ex] Cost\;\;per\;\;ticket = 2 * 44.35 \\[3ex] Cost\;\;per\;\;ticket = \$88.70 \\[3ex] R * 88.70 = 2483.60 \\[3ex] R = \dfrac{2483.6}{88.7} \\[5ex] R = 28\;tickets \\[3ex] (iv) \\[3ex] Total\;\;Cost\;\;of\;\;all\;\;tickets \\[3ex] = 130.50 + Q + 2483.60 \\[3ex] = 130.50 + 620.90 + 2483.60 \\[3ex] = \$3235.00 \\[3ex] 15\%\;\;tax \\[3ex] = \dfrac{15}{100} * 3235 \\[5ex] = 0.15(3235) \\[3ex] = \$485.25 $

(26.) ACT Rya and Sampath start running laps from the same starting line at the same time and in the same direction on a certain indoor track.
Rya completes one lap in $16$ seconds, and Sampath completes the same lap in $28$ seconds.
Both continue running at their same respective rates and in the same direction for $10$ minutes.
What is the fewest number of seconds after starting that Rya and Sampath will again be at their starting line at the same time?

$ F.\:\: 88 \\[3ex] G.\:\: 112 \\[3ex] H.\:\: 120 \\[3ex] J.\:\: 220 \\[3ex] K.\:\: 448 \\[3ex] $

The question is simply asking for the LCM (least common multiple) of $16$ and $28$ because of fewest number of seconds
Keep in mind that it is not just the common multiple of $16$ and $28$, but the least common multiple

$ \underline{Prime\;\;Factorization\;\;Method} \\[3ex] 16 = \color{black}{2} * \color{darkblue}{2} * 2 * 2 \\[3ex] 28 = \color{black}{2} * \color{darkblue}{2} * 7 \\[3ex] LCM = \color{black}{2} * \color{darkblue}{2} * 2 * 2 * 7 \\[3ex] LCM = 112 \\[3ex] $ The next time Rya and Sampath will again be at their starting line is $112$ seconds

(27.) ACT Jen is doing an experiment to determine whether a high-protein food affects the ability of white mice to find their way through a maze.
The mice is the experimental group were given the high-protein food; the mice in the control group were given regular food.
Jen then timed the mice as they found their way through the maze.
The table below shows the results.

Mouse number	Experimental group	Control group
$1$	$1$ min $46$ sec	$2$ min $13$ sec
$2$	$2$ min $2$ sec	$1$ min $49$ sec
$3$	$2$ min $20$ sec	$2$ min $28$ sec
$4$	$1$ min $51$ sec	$2$ min $7$ sec
$5$	$1$ min $41$ sec	$1$ min $58$ sec

The average time the mice in the experimental group took to find their way through the maze was how many seconds less than the average time taken by the mice in the control group?

$ A.\;\; 8 \\[3ex] B.\;\; 11 \\[3ex] C.\;\; 13 \\[3ex] D.\;\; 16 \\[3ex] E.\;\; 19 \\[3ex] $

We can solve this question in at least two ways.
Use any method you prefer.

$ 1\;min = 60\;sec \\[3ex] 2\;min = 2 * 60 = 120\;sec \\[3ex] 1\;min \;\; 46\;sec = 60 + 46 = 106\;sec \\[3ex] 2\;min \;\; 2\;sec = 120 + 2 = 122\;sec \\[3ex] 2\;min \;\; 20\;sec = 120 + 20 = 140\;sec \\[3ex] 1\;min \;\; 51\;sec = 60 + 51 = 111\;sec \\[3ex] 1\;min \;\; 41\;sec = 60 + 41 = 101\;sec \\[3ex] 2\;min \;\; 13\;sec = 120 + 13 = 133\;sec \\[3ex] 1\;min \;\; 49\;sec = 60 + 49 = 109\;sec \\[3ex] 2\;min \;\; 28\;sec = 120 + 28 = 148\;sec \\[3ex] 2\;min \;\; 7\;sec = 120 + 7 = 127\;sec \\[3ex] 1\;min \;\; 58\;sec = 60 + 58 = 118\;sec \\[3ex] $

1st Method: By Seconds
Mouse number	Experimental group	Experimental group (seconds)	Control group	Control group (seconds)
$1$	$1$ min $46$ sec	$106$	$2$ min $13$ sec	$133$
$2$	$2$ min $2$ sec	$122$	$1$ min $49$ sec	$109$
$3$	$2$ min $20$ sec	$140$	$2$ min $28$ sec	$148$
$4$	$1$ min $51$ sec	$111$	$2$ min $7$ sec	$127$
$5$	$1$ min $41$ sec	$101$	$1$ min $58$ sec	$118$
Sum:		$580$		$635$
Average:		$\dfrac{580}{5} = 116$		$\dfrac{635}{5} = 127$
Difference:		$127 - 116 = 11$

The average time the mice in the experimental group took to find their way through the maze is $11$ seconds less than the average time taken by the mice in the control group.

$ \underline{2nd\;\;Method} \\[3ex] \underline{Experimental\;\;Group} \\[3ex] Total\;\;time \\[3ex] = 1\;min \;\; 46\;sec \\[3ex] + 2\;min \;\; 2\;sec \\[3ex] + 2\;min \;\; 20\;sec \\[3ex] + 1\;min \;\; 51\;sec \\[3ex] + 1\;min \;\; 41\;sec \\[3ex] = ...\;min \;\; 160\;sec \\[3ex] /* \\[3ex] 60\;sec = 1\;min \\[3ex] 160\;sec = \dfrac{160 * 1}{60} = 2.666666667\;sec \\[3ex] Integer\;\;part = 2 \\[3ex] 2 * 60 = 120 \\[3ex] 160 - 120 = 40 \\[3ex] \therefore 160\;sec = 2\;min \;\; 40\;sec \\[3ex] */ \\[3ex] = 9\;min \;\; 40\;sec \\[3ex] Average\;\;time \\[3ex] = \dfrac{Total\;\;time}{sample\;\;size} \\[5ex] = \dfrac{9\;min \;\; 40\;sec}{5} \\[5ex] /* \\[3ex] 5\;\;divide\;\;9\;min = 1\;min \;\;remaining\;\; 4\;min \\[3ex] 5\;\; cannot\;\; divide\;\; 4\;min \\[3ex] 4\;min = 4 * 60 = 240\;sec \\[3ex] 240\;sec + 40\;sec = 280\;sec \\[3ex] 5\;\;divide\;\;240\;sec = 56\;sec \\[3ex] */ \\[3ex] = 1\;min \;\; 56\;sec \\[3ex] \underline{Control\;\;Group} \\[3ex] Total\;\;time \\[3ex] = 2\;min \;\; 13\;sec \\[3ex] + 1\;min \;\; 49\;sec \\[3ex] + 2\;min \;\; 28\;sec \\[3ex] + 2\;min \;\; 7\;sec \\[3ex] + 1\;min \;\; 58\;sec \\[3ex] = ...\;min \;\; 155\;sec \\[3ex] /* \\[3ex] 60\;sec = 1\;min \\[3ex] 155\;sec = \dfrac{155 * 1}{60} = 2.583333333\;sec \\[3ex] Integer\;\;part = 2 \\[3ex] 2 * 60 = 120 \\[3ex] 155 - 120 = 35 \\[3ex] \therefore 155\;sec = 2\;min \;\; 35\;sec \\[3ex] */ \\[3ex] = 10\;min \;\; 35\;sec \\[3ex] Average\;\;time \\[3ex] = \dfrac{Total\;\;time}{sample\;\;size} \\[5ex] = \dfrac{10\;min \;\; 35\;sec}{5} \\[5ex] /* \\[3ex] 5\;\;divide\;\;10\;min = 2\;min \\[3ex] 5\;\;divide\;\;35\;sec = 7\;sec \\[3ex] */ \\[3ex] = 2\;min \;\; 7\;sec \\[3ex] \underline{Difference} \\[3ex] Average\;\;time\;\;for\;\;Control\;\;Group - Average\;\;time\;\;for\;\;Experimental\;\;Group \\[3ex] = 2\;min \;\; 7\;sec - 1\;min \;\; 56\;sec \\[3ex] 7\;sec - 56\;sec \;\;results\;\;in\;\;a\;\;negative\;\;value \\[3ex] Borrow\;\;1\;min\;\;from\;\;2\;min \\[3ex] Remaining\;\; 1\;min \\[3ex] 1\;min = 60\;sec \\[3ex] Add\;\;60\;sec \;\;to\;\; 7\;sec \rightarrow 67\;sec \\[3ex] 67\;sec - 56\;sec = 11\;sec \\[3ex] 1\;min - 1\;min = 0\;min \\[3ex] $ The average time the mice in the experimental group took to find their way through the maze is $11$ seconds less than the average time taken by the mice in the control group.

(28.) ACT A retail sales associate's daily commission during $1$ week was $\$30$ on Monday and Tuesday and $\$70$ on Wednesday, Thursday, and Friday.
What was the associate's average daily commission for these $5$ days?

$ F.\:\: \$50 \\[3ex] G.\:\: \$51 \\[3ex] H.\:\: \$54 \\[3ex] J.\:\: \$55 \\[3ex] K.\:\: \$56 \\[3ex] $

$ \underline{Daily\;\;Commission} \\[3ex] Monday \rightarrow \$30 \\[3ex] Tuesday \rightarrow \$30 \\[3ex] Wednesday \rightarrow \$70 \\[3ex] Thursday \rightarrow \$70 \\[3ex] Friday \rightarrow \$70 \\[3ex] Average\;\;daily\;\;commission \\[3ex] = \dfrac{30 + 30 + 70 + 70 + 70}{5} \\[5ex] = \dfrac{270}{5} \\[5ex] = \$54.00 $

(29.) A controversial report by the U.S. Preventative Services Task Force recommends that women age 50 and over undergo a mammogram once every other year.
This report conflicts with the American Cancer Society's recommendations that women begin having yearly mammograms at age 40.
The percent of women under 40 who have breast cancer is under 2%.
Some argue that the number of false positives causes unnecessary biopsies and unneeded worry.
"Breast cancer in your breast doesn't kill you; the disease becomes deadly when it metastasizes, spreading to other organs or the bones... Curing it,... has been assumed to be a matter of finding and cutting out a tumor before... metastasis happens" (Orenstein, 2013).
The coming years may see a change in the pink ribbon campaign as although the number of deaths due to breast cancer has dropped by 25% since 1990, improved treatment, not early detection due to mammograms may be responsible.
(Source: Orenstein, P. "Our feel-good war on breast cancer." The New York Times. 25 April 2013. Retrieved from http://www.nytimes.com/2013/04/28/magazine/our-feel-good-war-on-breast-cancer.html?pagewanted=all&_r=0)

The table from the U.S. census shows the approximate number of females in the U.S. by age.

Age Range	Number of Females
20 — 24	9,223
25 — 29	9,326
30 — 34	9,896
35 — 44	22,670
45 — 54	18,741
55 — 64	12,250
65 — 4724	9,747
75 — 84	6,889
85+	2,099

Against the recommendations of the American Cancer Society, approximately how many women would be impacted by the change recommended by the U.S. Preventative Services Task Force?

U.S. Preventative Services Task Force's recommendation: 50 years and above
American Cancer Society's recommendation: 40 years and above
Age bracket of the women impacted by U.S. Preventative Services Task Force's recommendation: 40 – 50 years
But the age bracket was not given in the table
What we have is:
35 — 44: 22670
45 — 54: 18741
Assume a uniform distribution:

$ \underline{Midpoint} \\[3ex] \dfrac{35 + 44}{2} = 39.5 \approx 40\;years \\[5ex] \dfrac{45 + 54}{2} = 49.5 \approx 50\;years \\[5ex] \underline{Number\;\;of\;\;people} \\[3ex] 40 - 50 years \\[3ex] = \dfrac{22670}{2} + \dfrac{18741}{2} \\[5ex] = 11335 + 9370.5 \\[3ex] = 20705.5 \\[3ex] \approx 20706\;people $

(30.) ACT The DigiPhone Company advertises the following calling plans:

DigiPhone Calling Plans
600 minutes* for $89.99** per month 1,000 minutes* for $119.99** per month 1,400 minutes * for $149.99** per month
The charge for each additional minute is $0.20* **Taxes are NOT included.

Tanisha is on the $89.99 plan, and Suki is on the $119.99 plan.
To the nearest cent, how much more is the before-tax charge per minute for 600 minutes on Tanisha's plan than for 1,000 minutes on Suki's plan?

$ A.\;\; \$0.03 \\[3ex] B.\;\; \$0.12 \\[3ex] C.\;\; \$0.13 \\[3ex] D.\;\; \$0.15 \\[3ex] E.\;\; \$0.75 \\[3ex] $

$ \underline{Tanisha's\;\;plan} \\[3ex] time = 600\;\;minutes \\[3ex] cost = \$89.99 \\[3ex] charge\;\;per\;\;minute \\[3ex] = \dfrac{89.99}{600} \\[5ex] = \$0.1499833333/minute \\[5ex] \underline{Suki's\;\;plan} \\[3ex] time = 1000\;\;minutes \\[3ex] cost = \$119.99 \\[3ex] charge\;\;per\;\;minute \\[3ex] = \dfrac{119.99}{1000} \\[5ex] = \$0.11999\;\;per\;\;minute \\[5ex] \underline{Difference\;\;between\;\;the\;\;charges} \\[3ex] 0.1499833333 - 0.11999 \\[3ex] = 0.0299933333 \\[3ex] \approx \$0.03\;\;per\;\;minute $

(31.) Through the years, the geographical size of the states bordering the Great Lakes has shifted due to boundary changes and discrepancies in measuring the surface area of the lakes.
Boundary disputes and advances in technology are the primary sources of the changes in the total area of each of the lake bordering states.
The following table published in Minnesota History shows the area of Minnesota in square miles with the corresponding year.

Year	1860	1880	1906	1940	1990	2000	2013
Area	83,531	83,365	84,682	84,068	86,943	86,939	86,943

(Source: NETSTATE.com. 2013 Retrieved from http://www.netstate.com/states/geography/mn_geography.htm.)
Between which two year markers did the size of Minnesota in square miles experience the greatest change?

Change = New − Initial
Because we are interested in the greatest change, let us determine the absolute value of the change.
In other words, let us determine the absolute change.
Change = |New − Initial|

1860 and 1880: Change = |83365 − 83531| = |−166| = 166

1880 and 1960: Change = |84682 − 83365| = 1317

1906 and 1940: Change = |84068 − 84682| = |−614| = 614

1940 and 1990: Change = |86943 − 84068| = 2875

1990 and 2000: Change = |86939 − 86943| = |−4| = 4

2000 and 2013: Change = |86943 − 86939| = 4

Greatest change = 2875
The greatest change in square miles occured between 1940 and 1990

ACT Use the following information to answer Questions 33 - 35.
Many humans carry the gene Yq77.
The Yq test determines, with 100% accuracy, whether a human carries Yq77.
If a Yq test result is negative, the human does NOT carry Yq77
Sam designed a less expensive test for Yq77 called the Sam77 test.
It produces some incorrect results.
To determine the accuracy of the Sam77 test, both tests were administered to 1,000 volunteers.
The results from this administration are summarized in the table below.

	Positive Yq test	Negative Yq test
Positive Sam77 test Negative Sam77 test	590 25	10 375

(33.) It cost $2,500 to administer each Yq test and $50 to administer each Sam77 test.
What was the total cost to administer both tests to all the volunteers?

$ A.\;\; \$1,537,500 \\[3ex] B.\;\; \$1,556,750 \\[3ex] C.\;\; \$1,568,250 \\[3ex] D.\;\; \$2,500,000 \\[3ex] E.\;\; \$2,550,000 \\[3ex] $

$ Number\;\;of\;\;participants = 1000 \\[3ex] 1000\;\;Yq77\;\;tests\;\;@\;\;\$2500/test = 1000(2500) = 2,500,000 \\[3ex] 1000\;\;Sam77\;\;tests\;\;@\;\;\$50/test = 1000(50) = 50,000 \\[3ex] Total\;\;cost = \$2,500,000 + \$50,000 = \$2,550,000 $

(34.) What percent of the volunteers actually carry Yq77?

$ F.\;\; 57.5\% \\[3ex] G.\;\; 60.0\% \\[3ex] H.\;\; 60.5\% \\[3ex] J.\;\; 61.5\% \\[3ex] K.\;\; 62.5\% \\[3ex] $

$ Number\;\;of\;\;participants = 1000 \\[3ex] Number\;\;of\;\;positive\;\;Yq77\;\;test = 590 + 25 = 615 \\[3ex] \%\;\;of\;\;positive\;\;Yq77\;\;test \\[3ex] = \dfrac{615}{1000} * 100 \\[5ex] = 61.5\% $

(35.) For how many volunteers did the Sam77 test give an incorrect result?

$ A.\;\; 10 \\[3ex] B.\;\; 25 \\[3ex] C.\;\; 35 \\[3ex] D.\;\; 385 \\[3ex] E.\;\; 400 \\[3ex] $

Yq77 test is 100% accurate but Sam77 test is not.
So, an incorrect result by the Sam77 test implies that the:
(a.) volunteer had a positive Sam77 test but a negative Yq77 test (10 volunteers)
(b.) volunteer had a negative Sam77 test but a positive Yq77 test (25 volunteers)

10 + 25 = 35
This means that 35 volunteers received an incorrect result from the Sam77 test.

(37.) It takes someone 52 seconds to walk from the first (ground) floor of a building to the third floor.
How long will it take the person to walk from the first floor to the sixth floor (at the same pace, assuming all floors have the same height)?

Walking from the 1st floor to the third floor: 52 seconds
There are two intervals between the first floor and the third floor
This means that from 1st floor to 2nd floor (1st interval) and from 2nd floor to 3rd floor (2nd interval): 52 seconds
Assume equal proportion of times:

$\dfrac{52}{2} = 26$ seconds

1st floor to 2nd floor: 26 seconds
2nd floor to 3rd floor: 26 seconds
This means: 26 seconds per interval

At the same pace, how long will it take the person to walk from the first floor to the sixth floor?
first floor to sixth floor = 5 intervals (1st to 2nd, 2nd to 3rd, 3rd to 4th, 4th to 5th, and 5th to 6th)
Therefore, the time it will take the person to walk from the first floor to the sixth floor = 26(5) = 130 seconds.

(38.) ACT On the first day of school, Ms. Dubacek gave her third-grade students 6 new spelling words to learn.
On each day of school after that, she gave the students 3 new spelling words.
How many new spelling words had she given the students by the ends of the 21st day of school?

$ A.\;\; 60 \\[3ex] B.\;\; 63 \\[3ex] C.\;\; 66 \\[3ex] D.\;\; 69 \\[3ex] E.\;\; 72 \\[3ex] $

$ 1st\;\;day = 6\;\;new\;\;words \\[3ex] 2nd\;\;through\;\;21st\;\;day = 21 - 1 = 20\;\;days \\[3ex] 20\;\;days\;\;@\;\;3\;\;words\;\;per\;\;day = 20(3) = 60 \\[3ex] Total\;\;number\;\;of\;\;new\;\;words \\[3ex] = 6 + 60 = 66\;\;new\;\;words $

(39.) GCSE Here is some information, by ticket type, about the number of people visiting a cinema one week.

(a) How many children visited the cinema?
(b) How many more students than adults visited the cinema?
(c) A bar chart is drawn to show the number of people visiting the cinema one month.

Give one criticism of the bar chart.

$ Key:\;\;1\;box = 40\;people \\[3ex] (a) \\[3ex] Number\;\;of\;\;children \\[3ex] = 4\;boxes \\[3ex] = 4(40) \\[3ex] = 160\;people \\[3ex] (b) \\[3ex] Number\;\;of\;\;students \\[3ex] = 6\;boxes \\[3ex] = 6(40) \\[3ex] = 240\;people \\[3ex] Number\;\;of\;\;adults \\[3ex] = 3\dfrac{1}{2}\;boxes \\[5ex] = \dfrac{7}{2}(40) \\[5ex] = 7(20) \\[3ex] = 140\;people \\[3ex] More\;\;students\;\;than\;\;adults \\[3ex] = students - adults \\[3ex] = 240 - 140 \\[3ex] = 100\;people \\[3ex] $ (c)
The scale on the vertical axis (Number of people) is incorrect because 2500 is missing.
This implies that the number of Students is not represented correctly on the bar chart.

(40.) ACT A weeklong summer camp is held in June for children in Grades 3 - 6
Parents and guardians who enrolled their children for camp by May 15 received a 20% discount off the regular enrollment fee for each child enrolled.
For each grade, te table below gives the number of children enrolled by May 15 as well as the regular enrollment fee oer child.
The grade of any child is that child's grade in school as of May 15.

Grade	Enrollment by May 15	Regular enrollment fee
3 4 5 6	20 15 28 18	$350 $400 $450 $500

Top

(41.) Use the graph to answer the question.

Number 41-first

A. Taxpayers in the top 1% of income levels paid more money in income taxes than they would have without the tax cuts.
B. Taxpayers in the top 1% of income levels paid a greater percentage of total federal income tax revenue than they would have without the tax cuts.
C. Taxpayers in the top 1% of income levels paid 37% of total federal income tax revenue.
D. The treasury estimate if the share of tax cuts had not been enacted is 30%.

Remember to decide which is not true.
Notice it is not shown how much taxpayers paid before the tax cuts, and the bars in pink show an estimate for share if the tax cuts had not been enacted.
A. Taxpayers in the top 1% of income levels paid more money in income taxes than they would have without the tax cuts.

(42.) ACT One caution sign flashes every 4 seconds, and another caution sign flashes every 10 seconds.
At a certain instant, the 2 signs flash at the same time.
How many seconds elapse until the 2 signs next flash at the same time?

$ A.\;\; 6 \\[3ex] B.\;\; 7 \\[3ex] C.\;\; 14 \\[3ex] D.\;\; 20 \\[3ex] E.\;\; 40 \\[3ex] $

The question is asking for the Least Common Multiple (LCM) of 4 and 10

The colors besides red indicate the common factors that should be counted only one time.
Begin with them in the multiplication for the LCM.
Then, include the rest.

$ Numbers = 4, 10 \\[3ex] 4 = \color{black}{2} * 2 \\[3ex] 10 = \color{black}{2} * 5 \\[5ex] LCM = \color{black}{2} * 2 * 5 \\[3ex] LCM = 20 \\[3ex] $ 20 seconds will elapse until the 2 signs next flash at the same time

(43.) The table shows the (basketball) free throw percentages of two players in the first half and second half of a season.

**First Half**
Player	Free Throws Made	Attempts	Free throw (%)
Micah	30	93	............
Nahum	5	25	............

**Second Half**
Player	Free Throws Made	Attempts	Free throw (%)
Micah	19	33	............
Nahum	44	94	............

**Complete Season**
Player	Free Throws Made	Attempts	Free throw (%)
Micah	............	............	............
Nahum	............	............	............

(a.) For each player, fill in the free throw percentage (last column) for the first and second halves of the season.
(b.) Which player had the higher free throw percentage in the first half of the season?
(c.) Which player had the higher free throw percentage in the second half of the season?
(d.) For each player, fill in the table with the free throws made, attempts, and free throw percentage for the complete season.
(e.) Which player had the higher free throw percentage for the complete season?
(f.) Briefly explain why the results might seem surprising or paradoxical.

$ (a.) \\[3ex] \underline{1st\;\;Half} \\[3ex] Micah:\;\; \dfrac{30}{93} * 100 = 32.25806452\% \\[5ex] Nahum:\;\; \dfrac{5}{25} * 100 = 20\% \\[5ex] \underline{2nd\;\;Half} \\[3ex] Micah:\;\; \dfrac{19}{33} * 100 = 57.57575758\% \\[5ex] Nahum:\;\; \dfrac{44}{94} * 100 = 46.80851064\% \\[5ex] $ (b.) Micah had the higher free throw percentage in the first half of the season.

(c.) Micah had the higher free throw percentage in the second half of the season.

$ (d.) \\[3ex] \underline{Complete\;\;Season} \\[3ex] Micah: \\[3ex] Free\;\;Throws = 30 + 19 = 49 \\[3ex] Attempts = 93 + 33 = 126 \\[3ex] \dfrac{49}{126} * 100 = 38.88888889\% \\[5ex] Nahum \\[3ex] Free\;\;Throws = 5 + 44 = 49 \\[3ex] Attempts = 25 + 94 = 119 \\[3ex] \dfrac{49}{119} * 100 = 41.17647059\% \\[5ex] $ (e.) Nahum had the higher free throw percentage for the complete season.

(f.) Micah performed better in the first and second halves of the season, and yet Nahum outperformed Micah over the course of the entire season.
While both players took a similar number of shots overall, they took a different number of shots in each half of the season.

(44.) ACT One neon sign flashes every 6 seconds.
Another neon sign flashes every 8 seconds.
If they flash together and you begin counting seconds, how many seconds after they flash together will they next flash together?

$ F.\;\; 48 \\[3ex] G.\;\; 24 \\[3ex] H.\;\; 14 \\[3ex] J.\;\; 7 \\[3ex] K.\;\; 2 \\[3ex] $

Similar to Question (42.); the question is asking for the Least Common Multiple (LCM) of 6 and 8

The colors besides red indicate the common factors that should be counted only one time.
Begin with them in the multiplication for the LCM.
Then, include the rest.

$ Numbers = 6, 8 \\[3ex] 6 = \color{black}{2} * 3 \\[3ex] 8 = \color{black}{2} * 2 * 2 \\[5ex] LCM = \color{black}{2} * 3 * 2 * 2 \\[3ex] LCM = 24 \\[3ex] $ 24 seconds after they flash together, they will next flash together

(48.) ACT Karen invested $2,000 in a special savings account.
The balance of this special savings account will double every 5 years.
Assuming that Karen makes no other deposits and no withdrawals, what will be the balance of Karen's investment at the end of 40 years?

$ A.\;\; \$80,000 \\[3ex] B.\;\; \$256,000 \\[3ex] C.\;\; \$400,000 \\[3ex] D.\;\; \$512,000 \\[3ex] E.\;\; \$1,024,000 \\[3ex] $

double means multiplication by 2

$ initial\;\;amount = 2000 \\[5ex] At\;\;the\;\;end\;\;of\;\;5\;\;years: \\[3ex] updated\;\;amount = 2000(2) = 4000 \\[5ex] At\;\;the\;\;end\;\;of\;\;another\;\;5\;\;years\;(10\;\;years): \\[3ex] updated\;\;amount = 4000(2) = 8000 \\[5ex] At\;\;the\;\;end\;\;of\;\;another\;\;5\;\;years\;(15\;\;years): \\[3ex] updated\;\;amount = 8000(2) = 16000 \\[5ex] At\;\;the\;\;end\;\;of\;\;another\;\;5\;\;years\;(20\;\;years): \\[3ex] updated\;\;amount = 16000(2) = 32000 \\[5ex] At\;\;the\;\;end\;\;of\;\;another\;\;5\;\;years\;(25\;\;years): \\[3ex] updated\;\;amount = 32000(2) = 64000 \\[5ex] At\;\;the\;\;end\;\;of\;\;another\;\;5\;\;years\;(30\;\;years): \\[3ex] updated\;\;amount = 64000(2) = 128000 \\[5ex] At\;\;the\;\;end\;\;of\;\;another\;\;5\;\;years\;(35\;\;years): \\[3ex] updated\;\;amount = 128000(2) = 256000 \\[5ex] At\;\;the\;\;end\;\;of\;\;another\;\;5\;\;years\;(40\;\;years): \\[3ex] updated\;\;amount = 256000(2) = 512000 \\[3ex] $ The balance of Karen's investment at the end of 40 years is $512,000

(51.) The following table shows the number of hits (H), number of at-bats (AB), and batting average (AVGH = H/AB) for Major Leaguers Derek Jeter and David Justice in 1995 and 1996.

	1995			1996
Player	H	AB	AVG	H	AB	AVG
Jeter	12	48	0.250	183	582	0.314
Justice	104	411	0.253	45	140	0.321

(a.) Which player had the higher batting average in both 1995 and 1996?
(b.) Compute the batting average for each player for the two years combined.
(c.) Which player had the higher combined batting average for 1995 and 1996?
(d.) Briefly explain why the results might seem surprising or paradoxical.

$ 1995:\;\;AVG:\;\; 0.253 \gt 0.250 \\[3ex] 1996:\;\;AVG:\;\; 0.321 \gt 0.314 \\[3ex] $ (a.) David Justice had the higher batting average in both 1995 and 1996.

$ (b.) \\[3ex] Two\;\;years\;\;combined: \\[3ex] \underline{Derek\;\;Jeter} \\[3ex] H = 12 + 183 = 195 \\[3ex] AB = 48 + 582 = 630 \\[3ex] AVB = \dfrac{H}{AB} = \dfrac{195}{630} = 0.3095238095 \\[5ex] \underline{David\;\;Justice} \\[3ex] H = 104 + 45 = 149 \\[3ex] AB = 411 + 140 = 551 \\[3ex] AVB = \dfrac{H}{AB} = \dfrac{149}{551} = 0.2704174229 \\[3ex] $ (c.) Derek Jeter had the higher combined batting average for 1995 and 1996.

(d.) When the two seasons are taken separately, the data show that David Justice is the better hitter in both seasons.
When the two seasons are taken together, the data show that Derek Jeter is the better hitter overall.

(52.) ACT In 2011, the U.S Mint in Philadelphia produced 10,334,590,000 1-cent pieces, commonly called pennies.
These pennies were then bagged, with $50 in pennies per bag.
This process resulted in how many bags of pennies?
A. 2,066,918
B. 206,691,800
C. 5,167,295,000
D. 20,669,180,000
E. 51,672,950,000,000

$ \$1 = 100\;\;pennies \\[3ex] \implies \\[3ex] \$50 = 5000\;\;pennies = 1\;bag \\[3ex] \implies \\[3ex] Number\;\;of\;\;bags \\[3ex] = \dfrac{10,334,590,000}{5000} \\[5ex] = 2,066,918\;bags $

(54.) Decide whether these statements make sense (or is clearly true) or does not make sense (or is clearly false).
Explain your reasoning.

(I.) Our total class score is based only on homework and exams, and Student A has better scores than Student B on both homework and exams.
Therefore, Student A has a better overall score than Student B.

(II.) The Republicans claim the tax cut benefits everyone equally, but the Democrats say it favors the rich.
Clearly one side is lying.

(III.) Despite the fact that the new drug lowered blood pressure more than the old drug did in both the men and the women in the study, an overall analysis shows that the old drug was actually more effective.

(IV.) Baggage screening machines are 98% accurate in identifying bags that contain banned materials.
Therefore, if the screening shows a bag that contains banned materials, then it almost certainly does.

(I.) The statement does not make sense, because it is possible to appear better in each of two or more group comparisons but still be worse overall because of how the data are divided into unequally-sized groups.

(II.) The statement does not make sense because the two parties are using selective truth.
The Republicans are masking the change, where the Democrats are focused on the absolute change, but ignoring the fact that the wealthy pay most of the taxes.

(III.) The statement makes sense because there is no information given about the sampling method or about how the trials of the test were divided.

(IV.) The statement does not make sense because, depending on the proportion of true positives to total positives, the actual percentage of bags that show banned materials and actually have banned materials could be quite low.

(55.) Give an example explaining how politicians on both sides of an issue can use numbers to support their case without lying.
Fill in the dots.

Say a candidate is running for mayor of a city.
During the incumbent mayor's first year in office, the city had a population of 25,000, and 50 violent crimes were committed.
During the incumbent mayor's most recent year in office, the city had a population of 30,000, and 55 violent crimes were committed.
The ............ might argue that the number of crimes has ............, with ............ crime(s) having been committed during the incumbent mayor's most recent year in office compared to the incumbent mayor's first year in office.
The ............ might argue that the crime rate has ............, with a rate of 1 violent crime for every ............ people during the incumbent mayor's first year in office and a rate of 1 violent crime for every ............ people during the incumbent mayor's most recent year in office.
(Round to the nearest whole number as needed.)

$ \underline{Incumbent} \\[3ex] 1st\;\;year: \\[3ex] Population = 25000 \\[3ex] Violent\;\;crimes = 50 \\[3ex] Violent\;\;crimes\;\;per\;\;Population = \dfrac{50}{2500} = \dfrac{1}{500} \\[5ex] \implies \\[3ex] 1\;\;volent\;\;crime\;\;for\;\;every\;\;500\;\;people \\[5ex] Most\;\;recent\;\;year: \\[3ex] Population = 30000 \\[3ex] Violent\;\;crimes = 55 \\[3ex] Violent\;\;crimes\;\;per\;\;Population = \dfrac{55}{3000} = \dfrac{11}{6000} \approx \dfrac{1}{545.4545455} \approx \dfrac{1}{545} \\[5ex] \implies \\[3ex] 11\;\;volent\;\;crime\;\;for\;\;every\;\;6000\;\;people \\[3ex] \approx 1\;\;volent\;\;crime\;\;for\;\;every\;\;545\;\;people \\[5ex] Change\;\;in\;\;number\;\;of\;\;violent\;\;crimes \\[3ex] = New - Initial \\[3ex] = 55 - 50 = 5 \\[3ex] \implies \\[3ex] 5\;\;more\;\;violent\;\;crimes\;\;when\;\;most\;\;recent\;\;year\;\;is\;\;compared\;\;to\;\;1st\;\;year \\[3ex] $ Say a candidate is running for mayor of a city.
During the incumbent mayor's first year in office, the city had a population of 25,000, and 50 violent crimes were committed.
During the incumbent mayor's most recent year in office, the city had a population of 30,000, and 55 violent crimes were committed.
The new candidate might argue that the number of crimes has increased, with 5 more crime(s) having been committed during the incumbent mayor's most recent year in office compared to the incumbent mayor's first year in office.
The incumbent might argue that the crime rate has decreased, with a rate of 1 violent crime for every 500 people during the incumbent mayor's first year in office and a rate of 1 violent crime for every 545 people during the incumbent mayor's most recent year in office.

(56.) ACT Ricardo started a savings account for his daughter Ruth by depositing $500 into the account for her 1st birthday.
For each successive birthday, Ricardo deposits $200 more than the amount deposited for the previous birthday.
This is the only money deposited into the account.
What is the total amount of money Ricardo will have deposited into the account for Ruth up to and including her 6th birthday?

$ F.\;\; \$4,000 \\[3ex] G.\;\; \$4,200 \\[3ex] H.\;\; \$4,700 \\[3ex] J.\;\; \$4,900 \\[3ex] K.\;\; \$6,000 \\[3ex] $

$ \underline{1st\;\;birthday} \\[3ex] Deposit = 500 \\[5ex] \underline{2nd\;\;birthday} \\[3ex] Deposit = 200 + 500 = 700 \\[5ex] \underline{3rd\;\;birthday} \\[3ex] Deposit = 200 + 700 = 900 \\[5ex] \underline{4th\;\;birthday} \\[3ex] Deposit = 200 + 900 = 1100 \\[5ex] \underline{5th\;\;birthday} \\[3ex] Deposit = 200 + 1100 = 1300 \\[5ex] \underline{6th\;\;birthday} \\[3ex] Deposit = 200 + 1300 = 1500 \\[5ex] \underline{Total\;\;Deposited} \\[3ex] Total\;\;deposit \\[3ex] = 500 + 700 + 900 + 1100 + 1300 + 1500 \\[3ex] = 6000 \\[3ex] $ The total amount of money Ricardo will have deposited into the account for Ruth up to and including her 6th birthday is $6,000

(60.) ACT Mary takes 2 medications throughout the day and night.
One medication is to be taken every 6 hours and the other is to be taken every 4 hours.
If Mary begins taking both medications at 7:00 A.M. and takes both medications on schedule, how many hours later will it be when she next takes both medications at the same time?

$ F.\;\; 6 \\[3ex] G.\;\; 9 \\[3ex] H.\;\; 10 \\[3ex] J.\;\; 12 \\[3ex] K.\;\; 24 \\[3ex] $

We need to find the Least Common Multiple (LCM) of 6 and 4
The colors besides red indicate the common factors that should be counted only one time.
Begin with them in the multiplication for the LCM.
Then, include the rest.

$ Numbers = 6, 4 \\[3ex] 6 = \color{black}{2} * 3 \\[3ex] 4 = \color{black}{2} * 2 \\[5ex] LCM = \color{black}{2} * 3 * 2 \\[3ex] LCM = 12 \\[3ex] $ 12 hours later, Mary will take both medications at the same time.

If we are asked to find the actual time, then it will be:
7:00 AM + 12 hours
= 19
= 7:00 PM
At 7:00 PM, Mary will take both medications at the same time.

Top

(64.) ACT Two warning signs begin flashing at the same time.
One sign flashes every 3 seconds, and the other sign flashes every 8 seconds.
How many seconds elapse from the moment the 2 signs flash at the same time until they next flash at the same time?

$ F.\;\; 5 \\[3ex] G.\;\; 5.5 \\[3ex] H.\;\; 11 \\[3ex] J.\;\; 12 \\[3ex] K.\;\; 24 \\[3ex] $

The question is asking for the Least Common Multiple (LCM) of 3 and 8

$ Numbers = 3, 8 \\[3ex] 3 = 3 \\[3ex] 8 = 2 * 2 * 2 \\[5ex] LCM = 3 * 2 * 2 * 2 \\[3ex] LCM = 24 \\[3ex] $ 24 seconds elapse from the moment the 2 signs flash at the same time until they next flash at the same time

(68.) ACT One welcome sign flashes every 8 seconds, and another welcome sign flashes every 12 seconds.
At a certain instant, the 2 signs flash at the same time.
How many seconds elapse until the 2 signs next flash at the same time?

$ A.\;\; 4 \\[3ex] B.\;\; 10 \\[3ex] C.\;\; 20 \\[3ex] D.\;\; 24 \\[3ex] E.\;\; 96 \\[3ex] $

We need to find the Least Common Multiple (LCM) of 8 and 12
The colors besides red indicate the common factors that should be counted only one time.
Begin with them in the multiplication for the LCM.
Then, include the rest.

$ Numbers = 8, 12 \\[3ex] 8 = \color{black}{2} * \color{darkblue}{2} * 2 \\[3ex] 12 = \color{black}{2} * \color{darkblue}{2} * 3 \\[5ex] LCM = \color{black}{2} * \color{darkblue}{2} * 2 * 3 \\[3ex] LCM = 24 \\[3ex] $ 24 seconds elapse until the 2 signs next flash at the same time

ACT Use the following information to answer questions 71 – 73
The Dow Jones Industrial Average (DJIA) is an index of stock values.
The chart below gives the DJIA closing values from August 24 through September 30 of a certain year and the change in the closing value from the previous day.
A minus sign indicates a decline (a closing value less than the previous day's closing value).
A plus sign indicates an advance (a closing value greater than the previous day's closing value).

Dow Jones Industrial Average Closing Values
Date	Closing value	Change	Date	Closing value	Change
8/24 8/25 8/26 8/27 8/30 8/31 9/01 9/02 9/03 9/07 9/08 9/09 9/10	8,600 8,515 8,160 8,050 7,540 7,825 7,780 7,680 7,640 8,020 7,860 8,045 7,795	-85 -355 -110 -510 +285 -45 -100 -40 +380 -160 +185 -250	9/13 9/14 9/15 9/16 9/17 9/20 9/21 9/22 9/23 9/24 9/27 9/28 9/29 9/30	7,945 8,020 8,090 7,870 7,895 7,930 7,900 8,150 8,000 8,025 8,110 8,080 7,845 7,630	+150 +75 +70 -220 +25 +35 -30 +250 -150 +25 +85 -30 -235 -215

(71.) Which of the following is closest to the percent of decrease from the August 24 closing value to the September 30 closing value?

$ A.\;\; 7.9\% \\[3ex] B.\;\; 8.9\% \\[3ex] C.\;\; 11.3\% \\[3ex] D.\;\; 12.7\% \\[3ex] E.\;\; 88.7\% \\[3ex] $

$ 8/24:\;\; initial = 8600 \\[3ex] 9/30:\;\; new = 7,630 \\[3ex] change = new - initial \\[3ex] change = 7630 - 8600 = -970 \\[3ex] The\;\;change\;\;is\;\;a\;\;decrease \\[3ex] \%\;decrease = \dfrac{change}{initial} * 100 \\[5ex] \%\;decrease \\[3ex] = \dfrac{970}{8600} * 100 \\[5ex] = 11.27906977\% \\[3ex] \approx 11.3\% $

(72.) The chart shows 4 more declines than advances.
All of the following statements are true.
Which one best explains why the decline from the August 24 closing value to the September 30 closing value was relatively large?
F. The greatest change in the chart was a decline.
G. The least change in the chart was an advance.
H. The greatest number of consecutive declines was greater than the greatest number of consecutive advances.
J. The first change was a decline.
K. The average of the declines was much greater than the average of the advances.

In other words, which of the options best explains why the decline from the August 24 closing value to the September 30 closing value was relatively large (-970)?
All of the options are correct. However, which option is the most correct?
As observed and also written, there are more declines than advances.
But, the main reason for the large decline is because the average of the declines is much greater than the average of the advances.

Ask students to verify that statement...the last option...Option K. by calculating the:
(i.) average of the declines
(ii.) average of the advances

(73.) What is the average closing value for the 5-day period from September 13 through September 17?

$ A.\;\; 7,895 \\[3ex] B.\;\; 7,920 \\[3ex] C.\;\; 7,964 \\[3ex] D.\;\; 7,980 \\[3ex] E.\;\; 8,090 \\[3ex] $

$ 9/13:\;\; 7945 \\[3ex] 9/14:\;\; 8020 \\[3ex] 9/15:\;\; 8090 \\[3ex] 9/16:\;\; 7870 \\[3ex] 9/17:\;\; 7895 \\[3ex] Average\;\;closing\;\;value\;\;for\;\;the\;\;5-day\;\;period \\[3ex] = \dfrac{7945 + 8020 + 8090 + 7870 + 7895}{5} \\[5ex] = \dfrac{39820}{5} \\[5ex] = 7964 $

Top

Tests
In testing for marijuana and for most applicable tests:

(1.) A False Positive means that the applicant did not use it but tested positive for it.
ome examples of false positive tests and the causes are found here: https://www.webmd.com/drug-medication/ss/slideshow-drugs-false-positive-test (WebMD)

(2.) A False Negative means that the applicant used it but tested negative for it.

(3.) A True Positive means that the applicant used it and tested positive for it.

(4.) A True Negative means that the applicant did not use it and tested negative for it.

(85.) Indicate whether this case is true positive, true negative, false positive, or false negative.
Give reasons for your answer.

Case: Court Verdict: Suspect A murdered her daughter.
The murder was ruled as death by undetermined means.
The prosecution team could not provide convincing evidence that she was guilty.
The defense team convinced the jury that she was innocent.
The jury acquitted her.

This is a case of false negative
Suspect $A$ actually murdered her daughter.
However, because the prosecution team could not provide substantial evidence that she murdered her daughter, the jury acquitted her.

NOTE: This is similar to Type $II$ error in Statistics (Errors in Hypothesis Tests): Acquitting a guilty person

(86.) Indicate whether this case is true positive, true negative, false positive, or false negative.
Give reasons for your answer.

Case: Secondhand Marijuana Smoke: Augustine hangs out frequently with a friend who smokes pot.
THC (Tetrahydrocannbinol) is a chemical found in pot (cannabis plants).
A urine test done immediately after he visited his friend showed traces of THC.
He vehemently denied smoking pot and requested for a second test.

This is a case of false positive
This means that he did not smoke cannabis but tested positive for it.
Augustine did not actually smoke cannabis but tested positive for it because he probably inhaled it from his friend.

(87.) Indicate whether this case is true positive, true negative, false positive, or false negative.
Give reasons for your answer.

Case: Court Verdict: A record-breaking number of people were exonerated in 2015 — freed after serving time in American prisons for crimes they did not commit.: NBC News - February 3, 2016
One such case was that of William Vasquez who was cleared in December of an arson that killed a mother and her five children in 1981.

This is a case of false positive
This means that he did not commit the crime but was jailed for it.

NOTE: This is similar to Type $I$ error in Statistics (Errors in Hypothesis Tests): Convicting an innocent person

(88.) Indicate whether this case is true positive, true negative, false positive, or false negative.
Give reasons for your answer.

Case: Early Menstrual Period: Menstruation usually occurs on average of 14 days after ovulation.
However, Felicity noticed an early menstrual period and decided to take a home pregnancy test.
The test was negative.
But, she was convinced that she was pregant.
So, she waited a few days and tested again in the morning.

This is a case of false negative
Felicty was pregnant.
However, she probably did not have a high enough blood and urine pregnancy hormone (HCG: Human Chorionic Gonadotropin) level to get a positive pregnancy test.

(89.) Use the table to answer the question.

	Tumor is Malignant	Tumor is Benign	Total
Positive Mammogram	91 true positives	1492 false positives	1583
Negative Mammogram	10 false negatives	8381 true negatives	8391
Total	101	9873	9974

What was the total number of females whose tests gave incorrect results?

The total number of females whose tests gave incorrect results are the false positives and the the false negatives
This is equal to: 1492 + 10 = 1502 females

(90.) Explain how it is possible for a very accurate polygraph or drug test to result in a large proportion of false accusations.
Suppose a positive result is that the test results show not lying/no drug use.
Also, assume the probability of lying/drug use is very low.

A. Since the probabilities of both a false negative and a true negative are very high, the proportion of false negatives to total negatives will be low.
B. Since the probabilities of both a false positive and a true positive are very low, the proportion of false positives to total positives will be large.
C. Since the probabilities of both a false negative and a true negative are very low, the proportion of false negatives to total negatives will be large.

Recall that accuracy describes how closely a measurement approximates a true value.
An accurate measurement is very close to the true value.
If a test is P% accurate, then P% of the time, the approximated value is correct, while (100 − P)% of the time the approximated value is not correct.
Suppose that a drug test is 95% accurate and that of the 1000 people tested, 2% actually use drugs.
In this situation, 20 of the people use drugs and the remaining 980 people do not.
Of those who use drugs, 19 test positive and 1 tests negative.
Of those who do not use drugs, 49 test positive and 931 test negative.
This means that a total of 19 + 49 = 68 people test positive for drug use.
But 49 of these people, or $\dfrac{49}{68} * 100 = 72.05882353\%$

Thus, there is a large proportion of false accusations despite the 95% accuracy of the drug test.
C. Since the probabilities of both a false negative and a true negative are very low, the proportion of false negatives to total negatives will be large.

Top