Solved Examples: Compound Interest

Formulas Used: Mathematics of Finance

NOTE: Unless instructed otherwise;
For all financial calculations, do not round until the final answer.
Do not round intermediate calculations. If it is too long, write it to "at least" $5$ decimal places.
Round your final answer to $2$ decimal places.
Make sure you include your unit.

Solve all questions.
Use at least two methods where applicable.
Show all work.

For ACT Students
The ACT is a timed exam...60 questions for 60 minutes
This implies that you have to solve each question in one minute.
Some questions will typically take less than a minute a solve.
Some questions will typically take more than a minute to solve.
The goal is to maximize your time. You use the time saved on those questions you solved in less than a minute, to solve the questions that will take more than a minute.
So, you should try to solve each question correctly and timely.
So, it is not just solving a question correctly, but solving it correctly on time.
Please ensure you attempt all ACT questions.
There is no negative penalty for any wrong answer.

For JAMB and CMAT Students
Calculators are not allowed. So, the questions are solved in a way that does not require a calculator.

For NSC Students
For the Questions:
Any space included in a number indicates a comma used to separate digits...separating multiples of three digits from behind.
Any comma included in a number indicates a decimal point.
For the Solutions:
Decimals are used appropriately rather than commas
Commas are used to separate digits appropriately.

(1.) ACT When a bank pays $I\%$ interest, compounded annually, a deposit of $\$P$ increases to $\$P\left(1 + \dfrac{I}{100}\right)^y$ at the end of $y$ years, where $y$ is a whole number.
Lou initially deposits $\$600$ in an account that pays $4.75\%$ interest compounded annually.
Lou does not make any further deposits or withdrawals.
How much money, in dollars, is in Lou's account after $8$ years?

$ A.\:\: 6 * (1 + 4.75)^8 \\[3ex] B.\:\: 6 * (1 + 0.0475)^8 \\[3ex] C.\:\: 600 * (1 + 4.75)^8 \\[3ex] D.\:\: 600 * (1 + 0.0475)^8 \\[3ex] E.\:\: 600 * (1 + 0.0475) * 8 \\[3ex] $

$ P = 600 \\[3ex] I = 4.75\% \\[3ex] \dfrac{I}{100} = \dfrac{4.75}{100} = 0.0475 \\[5ex] y = 8 \\[3ex] Amount = P\left(1 + \dfrac{I}{100}\right)^y \\[5ex] \therefore Amount = 600 * (1 + 0.0475)^8 $

(2.) ACT Sara and Behzad are saving to make a down payment on a house.
With an initial deposit of $8,000, they have opened an account that compounds interest at an annual rate of 2.1%.
Assuming that Sara and Behzad make no additional deposits or withdrawals, which of the following expressions gives the dollar value of the account 4 years after the initial deposit?
(Note: For an account with an initial deposit of P dollars that compounds interest at an annual rate of r%, the value of the account t years after the initial deposit is $P\left(1 + \dfrac{r}{100}^t\right)$ dollars.)

$ F.\;\; 8,000(1.021)^4 \\[3ex] G.\;\; 8,000(1.21)^4 \\[3ex] H.\;\; 8,000(3.1)^4 \\[3ex] J.\;\; 8,000(121)^4 \\[3ex] K.\;\; 8,000 + 8,000(0.21)^4 \\[3ex] $

$ P = \$8000 \\[3ex] r = 2.1\% \\[3ex] t = 4\;years \\[3ex] Value\;\;of\;\;the\;\;account \\[3ex] = P\left(1 + \dfrac{r}{100}^t\right) \\[5ex] = 8000\left(1 + \dfrac{2.1}{100}^4\right) \\[5ex] = 8000(1 + 0.021)^4 \\[3ex] = 8000(1.021)^4 $

(3.) Habakkuk wants to have $\$16000$ in the future.
He intends to deposit some money in a company that pays $9\%$ interest rate compounded semiannually.
(a.) How much should he deposit $5$ years from now?
(b.) How much should he deposit $10$ years from now?

The question is asking us to calculate the principal.

$ (a.) \\[3ex] A = 16000 \\[3ex] r = 9\% = \dfrac{9}{100} = 0.09 \\[5ex] m = 2 \:\:(compounded\:\: semiannually) \\[3ex] t = 5 \\[3ex] P = \dfrac{A}{\left(1 + \dfrac{r}{m}\right)^{mt}} \\[7ex] P = \dfrac{16000}{\left(1 + \dfrac{0.09}{2}\right)^{2 * 5}} \\[7ex] P = \dfrac{16000}{(1 + 0.045)^{10}} \\[5ex] P = \dfrac{16000}{(1.045)^{10}} \\[5ex] P = \dfrac{16000}{1.552969422} \\[5ex] P = 10302.84291 \\[3ex] P = \$10302.84 \\[3ex] $ He should deposit $\$10302.84$ now in order to earn $\$16000.00$ in $5$ years ceteris paribus

$ (b.) \\[3ex] A = 16000 \\[3ex] r = 9\% = \dfrac{9}{100} = 0.09 \\[5ex] m = 2 \:\:(compounded\:\: semiannually) \\[3ex] t = 10 \\[3ex] P = \dfrac{A}{\left(1 + \dfrac{r}{m}\right)^{mt}} \\[7ex] P = \dfrac{16000}{\left(1 + \dfrac{0.09}{2}\right)^{2 * 10}} \\[7ex] P = \dfrac{16000}{(1 + 0.045)^{20}} \\[5ex] P = \dfrac{16000}{(1.045)^{20}} \\[5ex] P = \dfrac{16000}{2.411714025} \\[5ex] P = 6634.285755 \\[3ex] P = \$6634.29 \\[3ex] $ He should deposit $\$6634.29$ now in order to earn $\$16000.00$ in $10$ years ceteris paribus

(4.) An investment of $520.00 was made for 63 months in a financial institution that gives an interest rate of 3.5%.
Calculate the amounts and the dividends of the investment if the interest rate is compounded:
(I.) Annually
(II.) Semiannually
(III.) Quarterly
(IV.) Monthly
(V.) Weekly
(VI.) Ordinary daily
(VII.) Exact daily

$ P = \$520.00 \\[3ex] t = 63\:months = \dfrac{63}{12} = 5.25\:years \\[5ex] r = 3.5\% = \dfrac{3.5}{100} = 0.035 \\[5ex] A = P\left(1 + \dfrac{r}{m}\right)^{mt} \\[5ex] (I.) \\[3ex] Annually \rightarrow m = 1 \\[3ex] A = 520\left(1 + \dfrac{0.035}{1}\right)^{1(5.25)} \\[5ex] A = 520(1 + 0.035)^{(5.25)} \\[4ex] A = 520(1.035)^{(5.25)} \\[4ex] A = 520(1.197944882) \\[3ex] A = 622.9313386 \\[3ex] A \approx \$622.93 \\[5ex] (II.) \\[3ex] Semiannually \rightarrow m = 2 \\[3ex] A = 520\left(1 + \dfrac{0.035}{2}\right)^{2(5.25)} \\[5ex] A = 520(1 + 0.0175)^{(10.5)} \\[4ex] A = 520(1.0175)^{(10.5)} \\[4ex] A = 520(1.19980699) \\[3ex] A = 623.899635 \\[3ex] A \approx \$623.90 \\[5ex] (III.) \\[3ex] Quarterly \rightarrow m = 4 \\[3ex] A = 520\left(1 + \dfrac{0.035}{4}\right)^{4(5.25)} \\[5ex] A = 520(1 + 0.00875)^{(21)} \\[4ex] A = 520(1.000875)^{(21)} \\[4ex] A = 520(1.200755273) \\[3ex] A = 624.3927418 \\[3ex] A \approx \$624.39 \\[5ex] (IV.) \\[3ex] Monthly \rightarrow m = 12 \\[3ex] A = 520\left(1 + \dfrac{0.035}{12}\right)^{12(5.25)} \\[5ex] A = 520(1 + 0.002916666667)^{(63)} \\[4ex] A = 520(1.002916667)^{(63)} \\[4ex] A = 520(1.201394002) \\[3ex] A = 624.7248812 \\[3ex] A \approx \$624.72 \\[5ex] (V.) \\[3ex] Weekly \rightarrow m = 52 \\[3ex] A = 520\left(1 + \dfrac{0.035}{52}\right)^{52(5.25)} \\[5ex] A = 520(1 + 0.0006730769231)^{(273)} \\[4ex] A = 520(1.000673077)^{(273)} \\[4ex] A = 520(1.20164108) \\[3ex] A = 624.8533613 \\[3ex] A \approx \$624.85 \\[5ex] (VI.) \\[3ex] Ordinary\:Daily \rightarrow m = 360 \\[3ex] A = 520\left(1 + \dfrac{0.035}{360}\right)^{360(5.25)} \\[5ex] A = 520(1 + 0.00009722222222)^{(1890)} \\[4ex] A = 520(1.000097222)^{(1890)} \\[4ex] A = 520(1.201704623) \\[3ex] A = 624.8864042 \\[3ex] A \approx \$624.89 \\[5ex] (VII.) \\[3ex] Exact\:Daily \rightarrow m = 365 \\[3ex] A = 520\left(1 + \dfrac{0.035}{365}\right)^{365(5.25)} \\[5ex] A = 520(1 + 0.00009589041096)^{(1916.25)} \\[4ex] A = 520(1.00009589)^{(1916.25)} \\[4ex] A = 520(1.20170477) \\[3ex] A = 624.8864806 \\[3ex] A \approx \$624.89 $

(5.) CSEC Mr Williams bought a plot of land for $40,000.
The value of the land appreciated by 7% each year.
Calculate the value of the land after a period of two years.

We can solve this question in two ways - by using Quantitative Reasoning and the Compound Interest Formula

$ \underline{First\:\:Method:\;\; Quantitative\:\:Reasoning} \\[3ex] Present\:\:value = \$40000 \\[3ex] Appreciation\:\:rate = 7\% = \dfrac{7}{100} = 0.07 \\[5ex] 1st\:\:year\:\:appreciation = 0.07(40000) = 2800 \\[3ex] New\:\:value = 40000 + 2800 = 42800 \\[3ex] 2nd\:\:year\:\:appreciation = 0.07(42800) = 2996 \\[3ex] Newest\:\:value = 42800 + 2996 = 45796 \\[3ex] $ The value of the land after two years is $\$45796.00$

This question can also be solved by the Compound Interest formula.
You can view it as $7\%$ interest compounded yearly/annually

$ \underline{Second\:\:Method:\;\; Compound\:\:Interest\:\:Formula} \\[3ex] P = 40000 \\[3ex] r = 7\% = \dfrac{7}{100} = 0.07 \\[5ex] t = 2\:years \\[3ex] m = 1 \\[3ex] A = ? \\[3ex] A = P\left(1 + \dfrac{r}{m}\right)^{mt} \\[5ex] A = 40000\left(1 + \dfrac{0.07}{1}\right)^{1(2)} \\[5ex] A = 40000(1 + 0.07)^2 \\[4ex] A = 40000(1.07)^2 \\[4ex] A = 40000(1.1449) \\[3ex] A = 45796 \\[3ex] $ The value of the land after two years is $\$45796.00$

Ask students their preferred method.
They should give reasons for their choices.

(6.) Five and a half years ago, Peter invested $\$20,000$ in a retirement fund that grew at the rate of $12.45\%$ per year compounded quarterly.
How much does he have in his account today?

$ t = 5\dfrac{1}{2}\: years = 5.5\: years \\[5ex] P = \$20000 \\[3ex] r = 12.45\% = \dfrac{12.45}{100} = 0.1245 \\[5ex] Compounded\:\:Quarterly \implies m = 4 \\[3ex] A = ? \\[3ex] A = P\left(1 + \dfrac{r}{m}\right)^{mt} \\[5ex] A = 20000 * \left(1 + \dfrac{0.1245}{4}\right)^{4(5.5)} \\[5ex] A = 20000(1 + 0.031125)^{22} \\[4ex] A = 20000(1.031125)^{22} \\[4ex] A = 20000(1.9626776) \\[3ex] A = 39253.552 \\[3ex] $ Peter has $\$39253.55$ in his account today.

(7.) How long will it take an investment of $10,000 to double if the investment earns interest at the rate of 10% per year compounded monthly?

$ P = \$10000 \\[3ex] A = double\:\:P = 2(10000) = \$20000 \\[3ex] r = 10\% = \dfrac{10}{100} = 0.1 \\[5ex] Compounded\:\:Monthly \implies m = 12 \\[3ex] t = ? \\[3ex] t = \dfrac{\log\left(\dfrac{A}{P}\right)}{m\log\left(1 + \dfrac{r}{m}\right)} \\[7ex] \dfrac{A}{P} = \dfrac{20000}{10000} = 2 \\[5ex] \dfrac{r}{m} = \dfrac{0.1}{12} = 0.0083333 \\[5ex] t = \dfrac{\log 2}{12 * \log(1 + 0.0083333)} \\[5ex] t = \dfrac{0.301029995}{12 * \log(1.0083333)} \\[5ex] t = \dfrac{0.301029995}{12 * 0.003604124} \\[5ex] t = \dfrac{0.301029995}{0.043249491} \\[5ex] t = 6.96031301 \\[3ex] t \approx 6.96 \\[3ex] $ It will take about 6.96 years for the investment of $10,000 to double at the rate of 10% per year compounded monthly.

(8.) CSEC A credit union pays 8% per annum compound interest on all fixed deposits.
A customer deposited $24,000 in an account.
Calculate the TOTAL amount of money in the account at the end of two years.

$ r = 8\% = \dfrac{8}{100} = 0.08 \\[5ex] P = \$24000 \\[3ex] A = ? \\[3ex] t = 2\:years \\[3ex] Compounded\:\:per\:\:annum \implies m = 1 \\[3ex] A = P\left(1 + \dfrac{r}{m}\right)^{mt} \\[5ex] A = P\left(1 + \dfrac{0.08}{1}\right)^{1(2)} \\[5ex] A = 24000(1 + 0.08)^2 \\[4ex] A = 24000(1.08)^2 \\[4ex] A = 24000(1.1664) \\[3ex] A = 27993.6 \\[3ex] $ The total amount of money in the account at the end of two years is $\$27,993.60$

(9.) Joseph launched his construction business in $2008$
The revenue of his firm for that year was $\$250,000$
The revenue grew by $25\%$ in $2009$ and by $35\%$ in $2010$
Joseph projected that the revenue growth for his firm in the next $3$ years will be at least $30\%$ per year.
How much does he expect his minimum revenue to be for $2013$?

We can solve this question in two ways - by using Quantitative Reasoning and the Compound Interest Formula
Please note that for the second method - using the Compound Interest formula, we have to begin with $2011$ up until $2013$ because those are the years when he expects a steady rate of increase
So, our principal will be the amount at the end of $2010$

$ \underline{First\:\:Method - Quantitative\:\:Reasoning} \\[3ex] In \\[3ex] 2008;\:\: revenue = \$250000 \\[3ex] 2009;\:\:25\% growth = \dfrac{25}{100} * 250000 = 0.25 * 250000 = 62500 \\[5ex] New\:\:revenue = 250000 + 62500 = 312500 \\[3ex] 2010;\:\:35\% growth = \dfrac{35}{100} * 312500 = 0.35 * 312500 = 109375 \\[5ex] New\:\:revenue = 312500 + 109375 = 421875 \\[3ex] 2011;\:\:30\% growth = \dfrac{30}{100} * 421875 = 0.3 * 421875 = 126562.50 \\[5ex] New\:\:revenue = 421875 + 126562.50 = 548437.50 \\[3ex] 2012;\:\:30\% growth = \dfrac{30}{100} * 548437.50 = 0.3 * 548437.50 = 164531.25 \\[5ex] New\:\:revenue = 548437.50 + 164531.25 = 712968.75 \\[3ex] 2013;\:\:30\% growth = \dfrac{30}{100} * 712968.75 = 0.3 * 712968.75 = 213890.625 \\[5ex] New\:\:revenue = 712968.75 + 213890.625 = 926859.375 \\[3ex] $ He should expect a minimum revenue of $\$926,859.38$ in $2013$

$ \underline{Second\:\:Method - Compound\:\:Interest\:\:Formula} \\[3ex] Beginning\:\:from\:\:2011 \\[3ex] r = 30\% = \dfrac{30}{100} = 0.3 \\[5ex] P = \$421875 \\[3ex] t = 3\:years \\[3ex] Compounded\:\:per\:\:year \implies m = 1 \\[3ex] A = P\left(1 + \dfrac{r}{m}\right)^{mt} \\[5ex] A = P\left(1 + \dfrac{0.3}{1}\right)^{1(3)} \\[5ex] A = 421875(1 + 0.3)^3 \\[4ex] A = 421875(1.3)^3 \\[4ex] A = 421875(2.197) \\[3ex] A = 926859.375 \\[3ex] $ He should expect a minimum revenue of $\$926,859.38$ in $2013$

(10.) JAMB If the population of a town was $240000$ in January $1998$ and it increased by $2\%$ each year, what would be the population of the town in January $2000$?

$ A.\:\: 480,000 \\[3ex] B.\:\: 249,696 \\[3ex] C.\:\: 249,600 \\[3ex] D.\:\: 244,800 \\[3ex] $

We can solve this question in two ways - by using Quantitative Reasoning and the Compound Interest Formula
Use any way that is faster for you.

$ \underline{First\:\:Method - Quantitative\:\:Reasoning} \\[3ex] From\:\:January,1998\:\:to\:\:January, 2000 \\[3ex] Population\:\:in\:\:1998 = 240000 \\[3ex] 2\%\:\:increase\:\:for\:\:1999 = \dfrac{2}{100} * 240000 = 2(2400) = 4800 \\[5ex] Population\:\:in\:\:1999 = 240000 + 4800 = 244800 \\[3ex] 2\%\:\:increase\:\:for\:\:2000 = \dfrac{2}{100} * 244800 = 2(2448) = 4896 \\[5ex] Population\:\:in\:\:2000 = 244800 + 4896 = 249696 \\[3ex] $ Ceteris paribus, the population of the town in January, $2000$ would be $249,696$ people

$ \underline{Second\:\:Method - Compound\:\:Interest\:\:Formula} \\[3ex] From\:\:January,1998\:\:to\:\:January, 2000 \implies 2\:years \\[3ex] P = 240000 \\[3ex] r = 2\% = \dfrac{2}{100} = 0.02 \\[5ex] t = 2\:years \\[3ex] m = 1 \\[3ex] A = ? \\[3ex] A = P\left(1 + \dfrac{r}{m}\right)^{mt} \\[5ex] A = 240000\left(1 + \dfrac{0.02}{1}\right)^{1(2)} \\[5ex] A = 240000(1 + 0.02)^2 \\[4ex] A = 240000(1.02)^2 \\[4ex] A = 240000(1.0404) \\[3ex] A = 249696 \\[3ex] $ Ceteris paribus, the population of the town in January, $2000$ would be $249,696$ people

Ask students their preferred method.
They should give reasons for their choices.

(11.) JAMB A man wishes to keep some money in a savings account at $25\%$ compound interest so that after $3$ years, he can buy a car for $₦150,000$
How much does he need to deposit now?

$ A.\:\: ₦112,000.50 \\[3ex] B.\:\: ₦96,000.00 \\[3ex] C.\:\: ₦85,714.28 \\[3ex] A.\:\: ₦76,800.00 \\[3ex] $

The question is asking us to calculate the principal.

$ r = 25\% = \dfrac{25}{100} = \dfrac{1}{4} \\[5ex] m = 1 \:\:(compounded\:\: annually) \\[3ex] t = 3 \\[3ex] A = 150000 \\[3ex] P = \dfrac{A}{\left(1 + \dfrac{r}{m}\right)^{mt}} \\[7ex] \dfrac{r}{m} = r \div m = \dfrac{1}{4} \div 1 = \dfrac{1}{4} \\[5ex] 1 + \dfrac{r}{m} = 1 + \dfrac{1}{4} = \dfrac{4}{4} + \dfrac{1}{4} = \dfrac{4 + 1}{4} = \dfrac{5}{4} \\[5ex] mt = 1(3) = 3 \\[3ex] \left(1 + \dfrac{r}{m}\right)^{mt} = \left(\dfrac{5}{4}\right)^3 = \dfrac{5^3}{4^3} \\[7ex] P = \dfrac{150000}{\dfrac{5^3}{4^3}} \\[7ex] P = 150000 \div \dfrac{5^3}{4^3} \\[7ex] = 150000 * \dfrac{4^3}{5^3} \\[7ex] = \dfrac{150000 * 64}{5 * 5 * 5} \\[5ex] = \dfrac{30000 * 64}{5 * 5} \\[5ex] = \dfrac{6000 * 64}{5} \\[5ex] = 1200 * 64 \\[3ex] = 76800 \\[3ex] $ He should deposit $ ₦76,800.00$ now in order to earn $₦150,000$ in $3$ years ceteris paribus.

(12.) CSEC Faye borrowed $\$9\:600$ at $8\%$ per annum compound interest.
(i) Calculate the interest on the loan for the first year.
At the end of the first year, she repaid $\$4\:368$.
(ii) How much did she still owe at the beginning of the second year?
(iii) Calculate the interest on the remaining balance for the second year.

$ P = \$9600 \\[3ex] r = 8\% = \dfrac{8}{100} = 0.08 \\[5ex] (i) \\[3ex] t = 1\:year \\[3ex] Compounded\:\:annually \rightarrow m = 1 \\[3ex] A = ? \\[3ex] CI = ? \\[3ex] A = P\left(1 + \dfrac{r}{m}\right)^{mt} \\[5ex] A = 9600\left(1 + \dfrac{0.08}{1}\right)^{1(1)} \\[5ex] = 9600(1 + 0.08)^{1} \\[4ex] = 9600(1.08)^{1} \\[4ex] = 9600(1.08) \\[3ex] A = 10368 \\[3ex] CI = A - P \\[3ex] CI = 10368 - 9600 \\[3ex] CI = \$768 \\[3ex] $ The interest on the loan for the first year is $\$768$

$ (ii) \\[3ex] \underline{End\:\:of\:\:First\:\:Year} \\[3ex] Repaid\:\: \$4368 \\[3ex] \underline{Beginning\:\:of\:\:Second\:\:Year} \\[3ex] Balance = A - 4368 \\[3ex] Balance = 10368 - 4368 \\[3ex] Balance = \$6000 \\[3ex] $ She still owes $\$6000$ at the beginning of the second year.

$ (iii) \\[3ex] \underline{Second\:\:Year} \\[3ex] Balance = P = \$6000 \\[3ex] r = 8\% = 0.08 \\[3ex] t = 1\:year \\[3ex] m = 1 \\[3ex] A = ? \\[3ex] CI = ? \\[3ex] A = P\left(1 + \dfrac{r}{m}\right)^{mt} \\[5ex] A = 6000\left(1 + \dfrac{0.08}{1}\right)^{1(1)} \\[5ex] = 6000(1 + 0.08)^{1} \\[4ex] = 6000(1.08)^{1} \\[4ex] = 6000(1.08) \\[3ex] A = 6480 \\[3ex] CI = A - P \\[3ex] CI = 6480 - 6000 \\[3ex] CI = \$480 \\[3ex] $ The interest on the remaining balance on the loan for the second year is $\$480$

(13.) Mr. Williams bought a plot of land for $\$40,000$.
The value of the land appreciated by $7\%$ each year.
Calculate the value of the land after a $30-year$ period.
Compare to Question $5$.
Do you see the importance of using the Compound Interest formula?

For this question, it is much better to use the Compound Interest Formula

$ P = 40000 \\[3ex] r = 7\% = \dfrac{7}{100} = 0.07 \\[5ex] t = 30\:years \\[3ex] m = 1 \\[3ex] A = ? \\[3ex] A = P\left(1 + \dfrac{r}{m}\right)^{mt} \\[5ex] A = 40000\left(1 + \dfrac{0.07}{1}\right)^{1(30)} \\[5ex] A = 40000(1 + 0.07)^{30} \\[4ex] A = 40000(1.07)^{30} \\[4ex] A = 40000(7.61225504) \\[3ex] A = 304490.202 \\[3ex] A \approx \$304,490.20 \\[3ex] $ The value of the land after thirty years is $\$304,490.20$

(14.) Five and a half years ago, Peter invested $\$20,000$ which is worth $\$39,253.55$ today if the rate is compounded quarterly.
What rate of interest is used?
Compare and confirm your answer with Question $(6.)$

$ t = 5\dfrac{1}{2}\: years = 5.5\: years \\[5ex] P = \$20000 \\[3ex] A = \$39253.55 \\[3ex] Compounded\:\:Quarterly \implies m = 4 \\[3ex] r = ? \\[3ex] r = m\left[\left(\dfrac{A}{P}\right)^{\dfrac{1}{mt}} - 1\right] \\[7ex] mt = 4(5.5) = 22 \\[3ex] \dfrac{1}{mt} = \dfrac{1}{22} = 0.0454545455 \\[5ex] \dfrac{A}{P} = \dfrac{39253.55}{20000} = 1.9626775 \\[5ex] \left(\dfrac{A}{P}\right)^{\dfrac{1}{mt}} = 1.9626775^0.0454545455 = 1.031125 \\[7ex] \left(\dfrac{A}{P}\right)^{\dfrac{1}{mt}} - 1 = 1.031125 - 1 = 0.031125 \\[7ex] m\left[\left(\dfrac{A}{P}\right)^{\dfrac{1}{mt}} - 1\right] = 4(0.031125) = 0.1245 \\[7ex] 0.1245\:\:to\:\:\% = 0.1245(100) = 12.45\% \\[3ex] r = 12.45\% \\[3ex] $ The rate of interest is $12.45\%$

(15.) The John's family spends $\$960$ per month on food.
How much would they spend on food per month if inflation occurs at the rate of $3\%$ per year over the next $5$ years?

$ P = 960 \\[3ex] r = 3\% = \dfrac{3}{100} = 0.03 \\[5ex] t = 5\:years \\[3ex] m = 1 \\[3ex] A = ? \\[3ex] A = P\left(1 + \dfrac{r}{m}\right)^{mt} \\[5ex] A = 960\left(1 + \dfrac{0.03}{1}\right)^{1(5)} \\[5ex] A = 960(1 + 0.03)^{5} \\[4ex] A = 960(1.03)^{5} \\[4ex] A = 960(1.159274074) \\[3ex] A = 1112.903111 \\[3ex] A \approx \$1,112.90 $

(16.) A woman just inherited $\$250,000$.
If she invests the money at $4.5\%$ at compound interest, what can she expect to have at the end of $15$ years when she retires?

Sometimes; if the question does not state that the interest is simple interest, then assume compound interest.

If the question does not state the number of compounded periods per year for which the interest is compounded, then assume that the interest is compounded annually.

$ \underline{Compound\:\:Interest} \\[3ex] P = \$250000 \\[3ex] r = 4.5\% = \dfrac{4.5}{100} = 0.045 \\[5ex] t = 15\:years \\[3ex] Compounded\:\:annually\rightarrow m = 1 \\[3ex] A = ? \\[3ex] A = P\left(1 + \dfrac{r}{m}\right)^{mt} \\[7ex] = 250000\left(1 + \dfrac{0.045}{1}\right)^{1 * 15} \\[7ex] = 250000(1 + 0.045)^{15} \\[5ex] = 250000(1.045)^{15} \\[5ex] = 250000(1.93528244) \\[3ex] = \$483820.61 \\[3ex] $ Ceteris paribus, she would expect to have $\$483,820.61$ at the end of $15$ years when she retires.

(17.) The consumption of solar energy is expected to increase by $7\%$ per year during the next decade.
Assume Sun Systems services the City of Surprise, Arizona.
By how much will the company need to increase its capacity in order to meet demand at the end of the decade?

$ r = 7\% = \dfrac{7}{100} = 0.07 \\[5ex] t = 10\:years \\[3ex] m = 1 \\[3ex] P = ? \\[3ex] A = ? \\[3ex] A = P\left(1 + \dfrac{r}{m}\right)^{mt} \\[5ex] A = P\left(1 + \dfrac{0.07}{1}\right)^{1(10)} \\[5ex] A = P(1 + 0.07)^{10} \\[4ex] A = P(1.07)^{10} \\[4ex] A = P(1.967151357) \\[3ex] A = 1.967151357P \\[3ex] Amount\:\:of\:\:increase = New - Initial \\[3ex] Amount\:\:of\:\:increase = A - P \\[3ex] Amount\:\:of\:\:increase = 1.967151357P - P \\[3ex] Amount\:\:of\:\:increase = 0.967151357P \\[3ex] Amount\:\:of\:\:increase\:\:as\:\:a\:\:percent \\[3ex] = 0.967151357P * 100 \\[3ex] = 96.7151357P\% \\[3ex] $ By the end of the decade, the company should increase its present capacity by about $96.72\%$

(18.) Esther's parents deposited a sum of $\$750$ in a prepaid college account.
How much is the value of this money after a period of sixteen years if it is invested at $3\%$ compounded annually?

$ A = ? \\[3ex] P = 750 \: dollars \\[3ex] t = 16 \: years \\[3ex] Compounded\:\:annually\rightarrow m = 1 \\[3ex] r = 3\% = \dfrac{3}{100} = 0.03 \\[5ex] A = P\left(1 + \dfrac{r}{m}\right)^{mt} \\[5ex] A = 750 * \left(1 + \dfrac{0.03}{1}\right)^{1 * 16} \\[7ex] = 750 * (1 + 0.03)^{16} \\[3ex] = 750 * (1.03)^{16} \\[3ex] = 750 * 1.60470644 \\[3ex] = 1203.52983 \\[3ex] A \approx \$1,203.53 \\[3ex] $ Ceteris paribus, the amount in the prepaid account at the end of sixteen years will be $\$1203.53$

(19.) The inflation rates in the United States economy for 2004 through 2007 are 2.3%, 2.7%, 3.4%, and 3.2% respectively.
What was the purchasing power of a dollar at the beginning of 2007 compared to that at the beginning of 2004?

We can solve this question in two ways.
Use any method you prefer.
First Method: Calculate the present value/principal for each year starting from $2004$

$ \underline{2004} \\[3ex] r = 2.3\% = \dfrac{2.3}{100} = 0.023 \\[5ex] t = 1\:year \\[3ex] m = 1 \\[3ex] A = \$1 \\[3ex] P = ? \\[3ex] P = \dfrac{A}{\left(1 + \dfrac{r}{m}\right)^{mt}} \\[7ex] P = \dfrac{1}{\left(1 + \dfrac{0.023}{1}\right)^{1 * 1}} \\[7ex] P = \dfrac{1}{(1 + 0.023)^{1}} \\[5ex] P = \dfrac{1}{(1.023)^{1}} \\[5ex] P = \dfrac{1}{1.023} \\[5ex] P = 0.977517106 \\[5ex] \underline{2005} \\[3ex] r = 2.7\% = \dfrac{2.7}{100} = 0.027 \\[5ex] t = 1\:year \\[3ex] m = 1 \\[3ex] A = \$1 \\[3ex] P = ? \\[3ex] P = \dfrac{A}{\left(1 + \dfrac{r}{m}\right)^{mt}} \\[7ex] P = \dfrac{1}{\left(1 + \dfrac{0.027}{1}\right)^{1 * 1}} \\[7ex] P = \dfrac{1}{(1 + 0.027)^{1}} \\[5ex] P = \dfrac{1}{(1.027)^{1}} \\[5ex] P = \dfrac{1}{1.027} \\[5ex] P = 0.973709834 \\[5ex] \underline{2006} \\[3ex] r = 3.4\% = \dfrac{3.4}{100} = 0.034 \\[5ex] t = 1\:year \\[3ex] m = 1 \\[3ex] A = \$1 \\[3ex] P = ? \\[3ex] P = \dfrac{A}{\left(1 + \dfrac{r}{m}\right)^{mt}} \\[7ex] P = \dfrac{1}{\left(1 + \dfrac{0.034}{1}\right)^{1 * 1}} \\[7ex] P = \dfrac{1}{(1 + 0.034)^{1}} \\[5ex] P = \dfrac{1}{(1.034)^{1}} \\[5ex] P = \dfrac{1}{1.034} \\[5ex] P = 0.967117988 \\[5ex] \underline{2007} \\[3ex] r = 3.2\% = \dfrac{3.2}{100} = 0.032 \\[5ex] t = 1\:year \\[3ex] m = 1 \\[3ex] A = \$1 \\[3ex] P = ? \\[3ex] P = \dfrac{A}{\left(1 + \dfrac{r}{m}\right)^{mt}} \\[7ex] P = \dfrac{1}{\left(1 + \dfrac{0.032}{1}\right)^{1 * 1}} \\[7ex] P = \dfrac{1}{(1 + 0.032)^{1}} \\[5ex] P = \dfrac{1}{(1.032)^{1}} \\[5ex] P = \dfrac{1}{1.032} \\[5ex] P = 0.968992248 \\[5ex] Purchasing\:\:power\:\:at\:\:the\:\:beginning\:\:of\:\:2007\:\:compared\:\:to\:\:the\:\:beginning\:\:of\:\:2004 \\[3ex] = 0.977517106 * 0.973709834 * 0.967117988 * 0.968992248 \\[3ex] = 0.891977061 \\[3ex] \approx \$0.89 \\[3ex] $ Second Method: Let the purchasing power of a dollar at the beginning of $2007$ compared to that at the beginning of $2004$ = $p$

$ \underline{2004} \\[3ex] r = 2.3\% = \dfrac{2.3}{100} = 0.023 \\[5ex] t = 1\:year \\[3ex] m = 1 \\[3ex] P = \$1 \\[3ex] A = ? \\[3ex] A = P\left(1 + \dfrac{r}{m}\right)^{mt} \\[5ex] A = 1\left(1 + \dfrac{0.023}{1}\right)^{1(1)} \\[5ex] A = 1(1 + 0.023)^{1} \\[4ex] A = 1(1.023)^{1} \\[4ex] A = 1(1.023) \\[3ex] A = 1.023 \\[5ex] \underline{2005} \\[3ex] r = 2.7\% = \dfrac{2.7}{100} = 0.027 \\[5ex] t = 1\:year \\[3ex] m = 1 \\[3ex] P = \$1 \\[3ex] A = ? \\[3ex] A = P\left(1 + \dfrac{r}{m}\right)^{mt} \\[5ex] A = 1\left(1 + \dfrac{0.027}{1}\right)^{1(1)} \\[5ex] A = 1(1 + 0.027)^{1} \\[4ex] A = 1(1.027)^{1} \\[4ex] A = 1(1.027) \\[3ex] A = 1.027 \\[5ex] \underline{2006} \\[3ex] r = 3.4\% = \dfrac{3.4}{100} = 0.034 \\[5ex] t = 1\:year \\[3ex] m = 1 \\[3ex] P = \$1 \\[3ex] A = ? \\[3ex] A = P\left(1 + \dfrac{r}{m}\right)^{mt} \\[5ex] A = 1\left(1 + \dfrac{0.034}{1}\right)^{1(1)} \\[5ex] A = 1(1 + 0.034)^{1} \\[4ex] A = 1(1.034)^{1} \\[4ex] A = 1(1.034) \\[3ex] A = 1.034 \\[5ex] \underline{2007} \\[3ex] r = 3.2\% = \dfrac{3.2}{100} = 0.032 \\[5ex] t = 1\:year \\[3ex] m = 1 \\[3ex] P = \$1 \\[3ex] A = ? \\[3ex] A = P\left(1 + \dfrac{r}{m}\right)^{mt} \\[5ex] A = 1\left(1 + \dfrac{0.032}{1}\right)^{1(1)} \\[5ex] A = 1(1 + 0.032)^{1} \\[4ex] A = 1(1.032)^{1} \\[4ex] A = 1(1.032) \\[3ex] A = 1.032 \\[5ex] (1.023)(1.027)(1.034)(1.032) * p = 1 \\[3ex] 1.121105062 * p = 1 \\[3ex] p = \dfrac{1}{1.121105062} \\[5ex] p = 0.8919770628 \\[3ex] p \approx \$0.89 \\[3ex] $ The purchasing power of a dollar at the beginning of $2007$ compared to that at the beginning of $2004$ is approximately eighty nine cents.

(20.) WASSCE A principal of GH¢5,600.00 was deposited for 3 years at compound interest.
If the interest earned was GH¢1,200.00, find, correct to 3 significant figures, the interest rate per annum.

$ P = 5600 \\[3ex] t = 3 \\[3ex] CI = 1200 \\[3ex] r = ? \\[3ex] CI = A - P \\[3ex] A - P = CI \\[3ex] A = CI + P \\[3ex] A = 1200 + 5600 = 6800 \\[3ex] per\:\: annum\:\: means\:\: compounded\:\: annually \\[3ex] m = 1 \\[3ex] r = m\left[\left(\dfrac{A}{P}\right)^{\dfrac{1}{mt}} - 1\right] \\[7ex] r = 1 * \left[\left(\dfrac{6800}{5600}\right)^{\dfrac{1}{1 * 3}} - 1\right] \\[7ex] r = \left(\dfrac{6800}{5600}\right)^{\dfrac{1}{3}} - 1 \\[5ex] r = (1.214285714)^{\dfrac{1}{3}} - 1 \\[5ex] r = \sqrt[3]{1.214285714} - 1 \\[3ex] r = 1.066858844 - 1 \\[3ex] r = 0.0668588443 \\[3ex] r \approx 0.0669 \;\;(to\;\;3\;s.f) \\[3ex] OR\;\;\;\; r \approx 6.69\% \;\;(to\;\;3\;s.f) $

Top

(21.) In the year 1985, a house was valued at $110,000
By the year 2005, the value had appreciated to $148,000

(a.) What was the annual growth rate between 1985 and 200?

(b.) Assume that the value continued to grow by the same percentage.
What was the value of the house in the year 2010?

This is a case of Annual Compound Interest (Interest compounded annually)

$ (a.) \\[3ex] P = \$110000 \\[3ex] A = \$148000 \\[3ex] t = 2005 - 1985 = 20\;years \\[3ex] Compounded\;\;annually \rightarrow m = 1 \\[3ex] r = ? \\[3ex] r = m\left[\left(\dfrac{A}{P}\right)^{\dfrac{1}{mt}} - 1\right] \\[7ex] r = 1 * \left[\left(\dfrac{148000}{110000}\right)^{\dfrac{1}{1 * 20}} - 1\right] \\[7ex] r = (1.345454545)^{\dfrac{1}{20}} - 1 \\[5ex] r = 1.345454545^{0.5} - 1 \\[3ex] r = 1.014947204 - 1 \\[3ex] r = 0.014947204 \\[3ex] r = 1.4947204\% \\[3ex] r \approx 1.49\% ...to\;\;2\;\;decimal\;\;places \\[3ex] (b.) \\[3ex] r = 0.014947204 \\[3ex] P = \$110000 \\[3ex] t = 2010 - 1985 = 25\; years \\[3ex] A = ? \\[3ex] m = 1\\[3ex] A = P\left(1 + \dfrac{r}{m}\right)^{mt} \\[5ex] A = 110000 * \left(1 + \dfrac{0.014947204}{1}\right)^{1 * 25} \\[5ex] A = 110000 * (1 + 0.014947204)^{25} \\[3ex] A = 110000 * (1.014947204)^{25} \\[3ex] A = 110000 * 1.449059731 \\[3ex] A = 159396.5704 \\[3ex] A \approx \$159,396.57 $

(22.) CMAT A certain amount of money invested at 10% per annum compound interest for two years became $Rs\:2000$.
What is the initial investment?

$ 1.\:\: Rs.\:856 \\[3ex] 2.\:\: Rs.\:1,625 \\[3ex] 3.\:\: Rs.\:1,653 \\[3ex] 4.\:\: Rs.\:1,275 \\[3ex] $

$ r = 10\% = \dfrac{10}{100} = \dfrac{1}{10} \\[5ex] m = 1 \\[3ex] t = 2 \\[3ex] A = 2000 \\[3ex] P = \dfrac{A}{\left(1 + \dfrac{r}{m}\right)^{mt}} \\[7ex] mt = 1 * 2 = 2 \\[3ex] \dfrac{r}{m} = r \div m = \dfrac{1}{10} \div 1 = \dfrac{1}{10} \\[5ex] 1 + \dfrac{r}{m} = 1 + \dfrac{1}{10} = \dfrac{10}{10} + \dfrac{1}{10} = \dfrac{10 + 1}{10} = \dfrac{11}{10} \\[5ex] \left(1 + \dfrac{r}{m}\right)^{mt} = \left(\dfrac{11}{10}\right)^2 = \dfrac{121}{100} \\[5ex] \rightarrow P = 2000 \div \dfrac{121}{100} \\[5ex] P = 2000 * \dfrac{100}{121} \\[5ex] P \approx 1,653 $

(23.) The impact of the recession of 2009 has seen an ensuing slow recovery which has lasted well into 2013.
Since the slowing of the recession, Americans have seen a small increase in disposable income averaging less than one percent a month in 2013.
Despite the small gains in income, Americans are looking to place more discretionary money into savings plans and investments than into vacations and luxury items.
(Source: Bureau of Economic Analysis - U.S. Department of Commerce. 2013. Retrieved from http://www.bea.gov/newsreleases/national/pi/pinewsrelease.htm)

If an individual saves $5,700 and elects to place the total dollar amount into a savings account earning 2.75% APR compounded monthly, how much will the original deposit grow to in 12 years?

$ \underline{Compound\:\:Amount\:\:Formula} \\[3ex] P = 5700 \\[3ex] r = 2.75\% = \dfrac{2.75}{100} = 0.0275 \\[5ex] Compounded\:\:monthly \rightarrow m = 12 \\[3ex] t = 12\:years \\[3ex] A = ? \\[3ex] A = P\left(1 + \dfrac{r}{m}\right)^{mt} \\[5ex] A = 5700\left(1 + \dfrac{0.0275}{12}\right)^{12(12)} \\[5ex] A = 5700(1 + 0.0022916667)^{144} \\[4ex] A = 5700(1.002291667)^{144} \\[4ex] A = 5700(1.39044307) \\[3ex] A = 7925.525499 \\[3ex] A \approx \$7925.53 $

(24.) ACT A formula used to compute the current value of a savings account is $A = P(1 + r)^n$, where A is the current value; P is the amount deposited; r is the rate of interest for 1 compounding period, expressed as a decimal; and n is the number of compounding periods.
Which of the following is closest to the value of a savings account after 5 years if $10,000 is deposited at 4% annual interest compounded yearly?

$ F.\;\; \$10,400 \\[3ex] G.\;\; \$12,167 \\[3ex] H.\;\; \$42,000 \\[3ex] J.\;\; \$52,000 \\[3ex] K.\;\; \$53,782 \\[3ex] $

$ P = \$10,000 \\[3ex] r = 4\% = \dfrac{4}{100} = 0.04 \\[5ex] n = 1(5) = 5\;years \\[3ex] A = P(1 + r)^n \\[3ex] A = 10000(1 + 0.04)^5 \\[3ex] A = 10000(1.04)^5 \\[3ex] A = 10000(1.216652902) \\[3ex] A = 12166.52902 \\[3ex] A \approx \$12,167 $

(25.) A philanthropist sets up an endowment (an account that provides ongoing funds from interest only) with $1.8 billion.
(a.) The endowment earns interest at an annual rate of 7.2% compounded monthly.
How much would she give away each year in interest alone (leaving the balance unchanged)?

(b.) If the annual rate drops to 6.5% but is still compounded monthly, does the account generate enough interest to make 120 annual donations of $1 million each?

(c.) Assume that instead of setting up an endowment, the philanthropist decides

(a.) This is a case of Compound Interest
We can do this question using at least two approaches.
Use any approach you prefer.
1st Approach: By Formula

Answer: Number25-1st

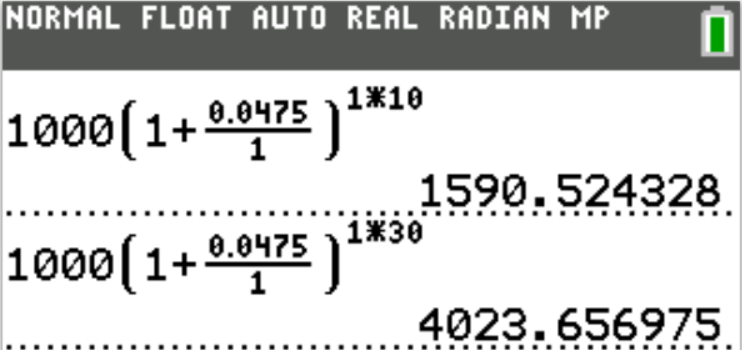
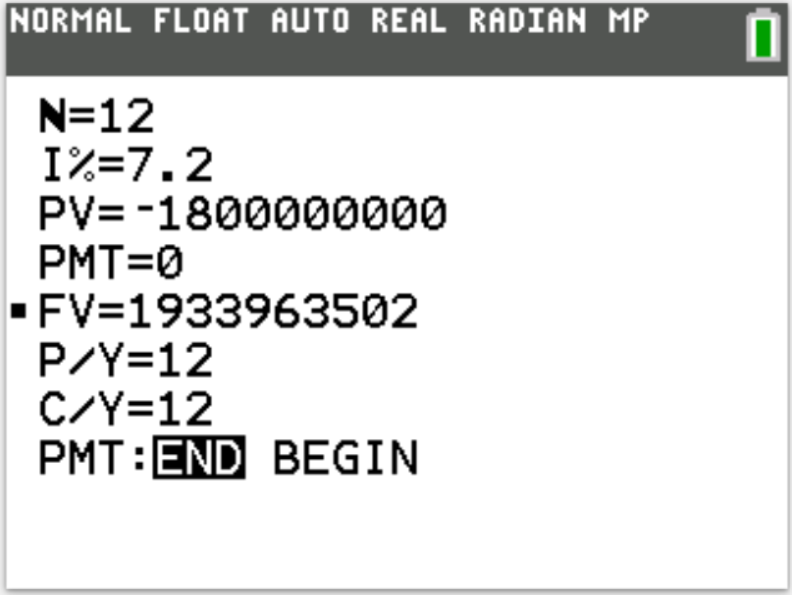
$ (a.) \\[3ex] \underline{Compound\:\:Amount\:\:Formula} \\[3ex] P = 1.8 * 10^9 \\[3ex] r = 7.2\% = \dfrac{7.2}{100} = 0.072 \\[5ex] Compounded\:\:monthly \rightarrow m = 12 \\[3ex] t = 1\:year \\[3ex] A = ? \\[3ex] A = P\left(1 + \dfrac{r}{m}\right)^{mt} \\[5ex] A = 1.8 * 10^9 * \left(1 + \dfrac{0.072}{12}\right)^{12(1)} \\[5ex] A = 1800000000(1 + 0.006)^{12} \\[4ex] A = 1800000000(1.006)^{12} \\[4ex] A = 1800000000(1.074424168) \\[3ex] A = \$1933963502 \\[5ex] \underline{Compound\:\:Interest\:\:Formula} \\[3ex] CI = A - P \\[3ex] CI = 1933963502 - 1800000000 \\[3ex] CI = \$133963502.00 \\[3ex] $ 2nd Approach: By Technology: Texas Instrument (TI) Finance App

Answer: Number25-2nd

$ (b.) \\[3ex] \underline{Compound\:\:Amount\:\:Formula} \\[3ex] P = 1.8 * 10^9 \\[3ex] r = 6.5\% = \dfrac{6.5}{100} = 0.065 \\[5ex] Compounded\:\:monthly \rightarrow m = 12 \\[3ex] t = 1\:year \\[3ex] A = ? \\[3ex] A = P\left(1 + \dfrac{r}{m}\right)^{mt} \\[5ex] A = 1.8 * 10^9 * \left(1 + \dfrac{0.065}{12}\right)^{12(1)} \\[5ex] A = 1800000000(1 + 0.0054166667)^{12} \\[4ex] A = 1800000000(1.005416667)^{12} \\[4ex] A = 1800000000(1.066971852) \\[3ex] A = \$1920549334 \\[5ex] \underline{Compound\:\:Interest\:\:Formula} \\[3ex] CI = A - P \\[3ex] CI = 1920549334 - 1800000000 \\[3ex] CI = \$120549333.60 \\[5ex] (c.) \\[3ex] Giving\;\;away\;\;\$1.8\;\;billion\;\;in\;\;7\;\;years \\[3ex] Amount\;\;per\;\;week\;\;is: \\[3ex] = \dfrac{1.8 * 10^9}{7\;years} * \dfrac{1\;year}{52\;weeks} \\[5ex] = 4945054.945 \\[3ex] \approx \$4945054.95 \;\;per\;\;week $

(26.) If the inflation rate is 2.95% compounded annually, how long will it take for prices to double?

We are not given the value of the principal
So, we can assume it to be $1
In that case, doubling $1
= 1 * 2
= 2
This implies that:
P = $1
A = $2

You can certainly do it that way.
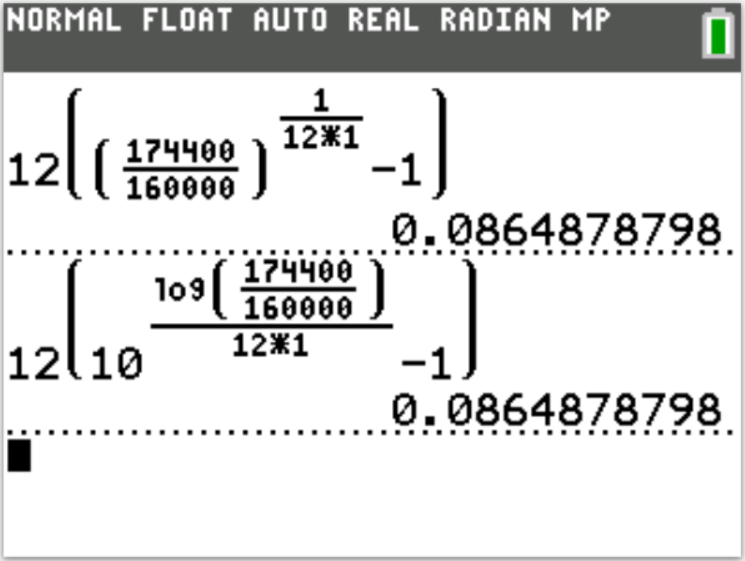
But I would like to do the question algebrically rather than arithmetically. $ r = 2.95\% = \dfrac{2.95}{100} = 0.0295 \\[5ex] Compounded\:\:annually\rightarrow m = 1 \\[3ex] P = P \\[3ex] A = 2P...double\:\:P \\[3ex] t = ? \\[3ex] t = \dfrac{\log\left(\dfrac{A}{P}\right)}{m\log\left(1 + \dfrac{r}{m}\right)} \\[7ex] t = \dfrac{\log\left(\dfrac{2P}{P}\right)}{1 * \log\left(1 + \dfrac{0.0295}{1}\right)} \\[7ex] t = \dfrac{\log 2}{1 * \log(1 + 0.0295)} \\[5ex] t = \dfrac{\log 2}{1 * \log(1.0295)} \\[5ex] t = \dfrac{\log 2}{\log(1.0295)} \\[5ex] t = \dfrac{0.3010299957}{0.01262635095} \\[5ex] t = 23.84140888 \\[3ex] t \approx 23.84\:years $

(27.) The following pair of investment plans are identical except for a small difference inn interest rates.
Compute the balance in the accounts after 10 and 30 years.
Discuss the difference.

Chang invests $1000 in a savings account that earns 4.5% compounded annually.
Kio invests $1000 in a different savings account that earns 4.75% compounded annually.

$ \underline{Chang's\;\;investment} \\[3ex] (a.) \\[3ex] P = \$1000 \\[3ex] r = 4.5\% = 0.045 \\[3ex] t = 10\;years \\[3ex] Compounded\;\;annually \implies m = 1 \\[3ex] (b.) \\[3ex] P = \$1000 \\[3ex] r = 4.5\% = 0.045 \\[3ex] t = 30\;years \\[3ex] Compounded\;\;annually \implies m = 1 \\[3ex] $ Number 27-1st

After 10 years, Chang will have a balance of approximately $1552.97
After 30 years, Chang will have a balance of approximately $3745.32

$ \underline{Kio's\;\;investment} \\[3ex] (a.) \\[3ex] P = \$1000 \\[3ex] r = 4.75\% = 0.0475 \\[3ex] t = 10\;years \\[3ex] Compounded\;\;annually \implies m = 1 \\[3ex] (b.) \\[3ex] P = \$1000 \\[3ex] r = 4.75\% = 0.0475 \\[3ex] t = 30\;years \\[3ex] Compounded\;\;annually \implies m = 1 \\[3ex] $ Number 27-2nd

After 10 years, Kio will have a balance of approximately $1590.52
After 30 years, Kio will have a balance of approximately $4023.66

$ \underline{Kio\;\;versus\;\;Chang} \\[3ex] Amount\;\;after\;\;10\;\;years \\[3ex] Initial = Chang's = 1552.969422 \\[3ex] New = Kio's = 1590.524328 \\[3ex] Change = Increase = 1590.524328 - 1552.969422 = 37.554906 \\[3ex] \%\;increase = \dfrac{Increase}{Initial} * 100 \\[5ex] = \dfrac{37.554906}{1552.969422} * 100 \\[5ex] = 2.418264357\% \\[5ex] Amount\;\;after\;\;30\;\;years \\[3ex] Initial = Chang's = 3745.318135 \\[3ex] New = Kio's = 4023.656975 \\[3ex] Change = Increase = 4023.656975 - 3745.318135 = 278.33884 \\[3ex] \%\;increase = \dfrac{Increase}{Initial} * 100 \\[5ex] = \dfrac{278.33884}{3745.318135} * 100 \\[5ex] = 7.431647459\% \\[3ex] $ Approximating all values to two decimal places:
After 10 years, Kio will have $37.55 or 2.42% more than Chang.
After 30 years, Kio will have $278.34 or 7.13% more than Chang.

(28.) Most people do not have the choice to drive or fly to a destination close to home but perhaps we will in the future.
Two companies, one in Massachusetts and one in Slovakia, are working on producing a flying car.
A prototype has entered the testing phase in Slovakia and the Massachusetts company is working on perfecting retractable wings on their car model.
Although mass production has not begun, the prototypes have successfully reached lift off with ranges of just over 400 miles and speeds just over 100 miles per hour.
(Source: Marquis, E. "Aeromobil 2.5 flying car makes first flight test." AolAutos. 25 Oct 2013. Retrieved from http://translogic.aolautos.com/2013/10/25/aeromobil-2-5-flying-car-makes-first-test-flight/)

Suppose the sticker price on a particular car was $17,090.
A consumer expects to qualify for a rebate of $4,500 and receive an additional $3,500 for trading in his current car.
Six years ago the consumer invested $7,500 in a savings account earning 2% APR compounded monthly.
To the nearest dollar how much would the consumer have saved to purchase the car?

$ P = \$7500 \\[3ex] t = 6\;years \\[3ex] Compounded\;\;Monthly \rightarrow m = 12 \\[3ex] r = 2\% = \dfrac{2}{100} = 0.02 \\[5ex] A = P\left(1 + \dfrac{r}{m}\right)^{mt} \\[5ex] A = 7500\left(1 + \dfrac{0.02}{12}\right)^{12(6)} \\[5ex] $ Number 28

$ A = 8455.381745 \\[3ex] A \approx \$8455.38 \\[3ex] $ Total saved would be $8455...rounded to the nearest dollar.

(30.) After two years, an investment with interest compounded annually and an APR of 6.3% increases in value by which factor?
Leave your answer in exponential notation.

$ Principal = P...initial\;\;value \\[3ex] t = 2\;years \\[3ex] m = 1 \\[3ex] r = 6.3\% = \dfrac{6.3}{100} = 0.063 \\[5ex] A = P\left(1 + \dfrac{r}{m}\right)^{mt} \\[5ex] A = P\left(1 + \dfrac{0.063}{1}\right)^{1(2)} \\[5ex] A = P(1 + 0.063)^2 \\[4ex] A = P(1.063)^2...new\;\;value \\[4ex] Increased\;\;by\;\;a\;\;factor\;\;of \\[3ex] 1.063^2 $

(32.) Consider two accounts earning compound interest, one with an APR of 10% and the other with an APR of 5%, both with the same initial deposit (and no further deposits or withdrawals).
After twenty years, how much more interest will the account with APR = 10% have earned than the account with APR = 5%?

Let us assume:
annual compounding of interest for both APRs: m = 1
APR of 10% = 1st Case
APR of 5% = 2nd Case
P for both cases = $1
t for both cases = 20 years

$ A = P\left(1 + \dfrac{r}{m}\right)^{mt} \\[5ex] \underline{1st\;\;Case} \\[3ex] r = 10\% = \dfrac{10}{100} = 0.1 \\[5ex] A = 1\left(1 + \dfrac{0.1}{1}\right)^{1(20)} \\[5ex] A = 1(1 + 0.1)^{20} \\[4ex] A = (1.1)^{20}...new\;\;value \\[4ex] A = 6.727499949 \\[3ex] CI = A - P \\[3ex] CI = 6.727499949 - 1 \\[3ex] CI = 5.727499949 \\[3ex] CI \approx \$5.73 \\[5ex] \underline{2nd\;\;Case} \\[3ex] r = 5\% = \dfrac{5}{100} = 0.05 \\[5ex] A = 1\left(1 + \dfrac{0.05}{1}\right)^{1(20)} \\[5ex] A = 1(1 + 0.05)^{20} \\[4ex] A = (1.05)^{20}...new\;\;value \\[4ex] A = 2.653297705 \\[3ex] CI = A - P \\[3ex] CI = 2.653297705 - 1 \\[3ex] CI = 1.653297705 \\[3ex] CI \approx \$1.65 \\[3ex] 5.727499949 \gt 1.653297705 \\[5ex] 5.727499949 \gt 2(1.653297705) \\[3ex] 5.727499949 \gt 3.30659541 \\[5ex] 5.727499949 \gt 3(1.653297705) \\[3ex] 5.727499949 \gt 4.959893115 \\[5ex] $ The account with APR = 10% will have earned More than twice as much than the account with APR = 5%.
The account with APR = 10% will have earned More than thrice as much than the account with APR = 5%.

(34.) How long will it take money to triple at an APR of 7.3% compounded annually?
Round up to the nearest year.

We are not given the value of the principal
So, we can assume it to be $1
In that case, tripling $1
= 1 * 3
= 3
This implies that:
P = $1
A = $3

You can certainly do it that way.
But I would like to do the question algebrically rather than arithmetically. $ r = 7.3\% = \dfrac{7.3}{100} = 0.073 \\[5ex] Compounded\:\:annually\rightarrow m = 1 \\[3ex] P = P \\[3ex] A = 3P...triple\:\:P \\[3ex] t = ? \\[3ex] t = \dfrac{\log\left(\dfrac{A}{P}\right)}{m\log\left(1 + \dfrac{r}{m}\right)} \\[7ex] t = \dfrac{\log\left(\dfrac{3P}{P}\right)}{1 * \log\left(1 + \dfrac{0.073}{1}\right)} \\[7ex] t = \dfrac{\log 3}{1 * \log(1 + 0.073)} \\[5ex] t = \dfrac{\log 3}{1 * \log(1.073)} \\[5ex] t = \dfrac{\log 3}{\log(1.073)} \\[5ex] t = \dfrac{0.4771212547}{0.030599722} \\[5ex] t = 15.59233954 \\[3ex] t \approx 16\:years $

(37.) Determine the accumulated balance after the stated periods.

(A.) $6,000 invested at an APR of 5% for 10 years
Interest is compounded annually.

(B.) $16,000 invested at an APR of 6% for 9 years
Interest is compounded quarterly.

(C.) $15,000 invested at an APR of 3% for 4 years
Interest is compounded daily.

(D.) $3,000 invested at an APR of 3.16% for 19 years
Interest is compounded monthly.

$ \underline{Compound\;\;Interest\;\;Formula} \\[3ex] A = P\left(1 + \dfrac{r}{m}\right)^{mt} \\[7ex] (A.) \\[3ex] P = \$6000 \\[3ex] r = 5\% = 0.05 \\[3ex] t = 10\;years \\[3ex] Compounded\;\;annually \implies m = 1 \\[3ex] $ Number 37A

$ A \approx \$9773.37 \\[5ex] (B.) \\[3ex] P = \$16000 \\[3ex] r = 6\% = 0.06 \\[3ex] t = 9\;years \\[3ex] Compounded\;\;quarterly \implies m = 4 \\[3ex] $ Number 37B

$ A \approx \$27346.23 \\[5ex] (C.) \\[3ex] P = \$15000 \\[3ex] r = 3\% = 0.03 \\[3ex] t = 4\;years \\[3ex] Compounded\;\;daily \implies m = 5 \\[3ex] $ Number 37C

$ A \approx \$16912.37 \\[5ex] (D.) \\[3ex] P = \$3000 \\[3ex] r = 3.16\% = 0.0316 \\[3ex] t = 19\;years \\[3ex] Compounded\;\;monthly \implies m = 12 \\[3ex] $ Number 37D

(38.) With the same deposit, APR, and length of time, an investment with monthly compounding will yield what amount?

A. The monthly compounding yields a smaller balance than an account with quarterly compounding because more compounding means a higher yield.

B. The monthly compounding yields a greater balance than an account with daily compounding because more compounding means a higher yield.

C. The monthly compounding yields a smaller balance than an account with quarterly compounding because more compounding means a lower yield.

D. The monthly compounding yields a greater balance than an account with daily compounding because more compounding means a lower yield.

E. The monthly compounding yields a greater balance than an account with annual compounding because more compounding means a lower yield.

F. The monthly compounding yields a greater balance than an account with annual compounding because more compounding means a higher yield.

F. The monthly compounding yields a greater balance than an account with annual compounding because more compounding means a higher yield.

(40.) How long will it take your initial deposit to grow by 50% at an APR of 7.6% compounded annually?

We are not given the value of the principal
So, we can assume it to be $1
In that case, growing $1 by 50%
= 1 + 50% * 1
= 1 + 0.5(1)
= 1 + 0.5
= 1.5
This implies that:
P = $1
A = $1.50

You can certainly do it that way.
But I would like to do the question algebrically rather than arithmetically.

$ r = 7.6\% = \dfrac{7.6}{100} = 0.076 \\[5ex] Compounded\:\:annually\rightarrow m = 1 \\[3ex] P = P \\[3ex] 50\%\;\;of\;\;P = 0.5(P) = 0.5P \\[3ex] Growing\:\:P\;\;by\;\;50\% = P + 0.5P = 1.5P \\[3ex] A = 1.5P \\[3ex] t = ? \\[3ex] t = \dfrac{\log\left(\dfrac{A}{P}\right)}{m\log\left(1 + \dfrac{r}{m}\right)} \\[7ex] t = \dfrac{\log\left(\dfrac{1.5P}{P}\right)}{1 * \log\left(1 + \dfrac{0.076}{1}\right)} \\[7ex] t = \dfrac{\log 1.5}{1 * \log(1 + 0.076)} \\[5ex] t = \dfrac{\log 1.5}{1 * \log(1.076)} \\[5ex] t = \dfrac{\log 1.5}{\log(1.076)} \\[5ex] t = 5.535324945 \\[3ex] t \approx 6\:years $

Top

(41.) A retired couple plans to supplement their Social Security with interest earned by a $160,000 retirement fund.

(a.) If the fund compounds interest monthly at an APR of 6.3%, which the couple takes out at the end of the year for spending in the next year, how much average interest is generated each month?

(b.) Suppose the APR drops to 3.9%.
What is the resulting average interest payment each month?

(c.) Estimate the APR needed to generate $1200 each month in average interest.

$ P = \$160,000 \\[3ex] (a.) \\[3ex] Compounded\;\;monthly \implies m = 12 \\[3ex] r = APR = 6.3\% = \dfrac{6.3}{100} = 0.063 \\[5ex] t = 1\;year \\[3ex] CI = ? \\[3ex] CI = A - P \\[3ex] A = ? \\[3ex] A = P\left(1 + \dfrac{r}{m}\right)^{mt} \\[5ex] A = 160000\left(1 + \dfrac{0.063}{12}\right)^{12(1)} \\[5ex] A = 170376.2142 \\[3ex] A \approx \$170376.21 \\[3ex] $ This is the compound amount per year.
Let us calculate the compound interest

$ CI = A - P \\[3ex] CI = 170376.2142 - 160000 \\[3ex] CI = 10376.21423 \\[3ex] CI \approx \$10376.21 \\[3ex] $ This is the compound interest per year.
Let us calculate the compound interest per month.

$ CI\;\;per\;\;month \\[3ex] = \dfrac{10376.21423}{12} \\[5ex] = 864.6845188 \\[3ex] \approx \$864.68 \\[3ex] $ Number 41-1st

$ (b.) \\[3ex] Compounded\;\;monthly \implies m = 12 \\[3ex] r = APR = 3.9\% = \dfrac{3.9}{100} = 0.039 \\[5ex] t = 1\;year \\[3ex] CI = ? \\[3ex] CI = A - P \\[3ex] A = ? \\[3ex] A = P\left(1 + \dfrac{r}{m}\right)^{mt} \\[5ex] A = 160000\left(1 + \dfrac{0.039}{12}\right)^{12(1)} \\[5ex] A = 166352.7572 \\[3ex] A \approx \$166352.76 \\[3ex] $ This is the compound amount per year.
Let us calculate the compound interest

$ CI = A - P \\[3ex] CI = 166352.7572 - 160000 \\[3ex] CI = 6352.757232 \\[3ex] CI \approx \$6352.76 \\[3ex] $ This is the compound interest per year.
Let us calculate the compound interest per month.

$ CI\;\;per\;\;month \\[3ex] = \dfrac{6352.757232}{12} \\[5ex] = 529.396436 \\[3ex] \approx \$529.40 \\[3ex] $ Number 41-2nd

$ (c.) \\[3ex] Compounded\;\;monthly \implies m = 12 \\[3ex] t = 1\;year \\[3ex] r = APR = ? \\[3ex] CI\;\;per\;\;month = \$1200 \\[3ex] CI\;\;per\;\;year = 1200(12) = \$14400 \\[3ex] A = P + CI \\[3ex] A = 160000 + 14400 \\[3ex] A = \$174400 \\[3ex] r = m\left[\left(\dfrac{A}{P}\right)^{\dfrac{1}{mt}} - 1\right] \\[10ex] r = 12\left[\left(\dfrac{174400}{160000}\right)^{\dfrac{1}{12 * 1}} - 1\right] \\[10ex] OR \\[3ex] r = m\left(10^{\dfrac{\log\left(\dfrac{A}{P}\right)}{mt}} - 1\right) \\[10ex] r = 12\left(10^{\dfrac{\log\left(\dfrac{174400}{160000}\right)}{12 * 1}} - 1\right) \\[10ex] $ Number 41-3rd

$ r = 0.0864878798 \\[3ex] r = 8.64878798\% $

(44.) $2000 is deposited in an account that pays an APR of 8.5% compounded annually.
How long will it take for the balance to reach $100,000?

$ r = 8.5\% = \dfrac{8.5}{100} = 0.085 \\[5ex] Compounded\:\:annually\rightarrow m = 1 \\[3ex] P = \$2000 \\[3ex] A = \$100000 \\[3ex] t = ? \\[3ex] t = \dfrac{\log\left(\dfrac{A}{P}\right)}{m\log\left(1 + \dfrac{r}{m}\right)} \\[7ex] t = \dfrac{\log\left(\dfrac{100000}{2000}\right)}{1 * \log\left(1 + \dfrac{0.085}{1}\right)} \\[7ex] t = \dfrac{\log (50)}{1 * \log(1 + 0.085)} \\[5ex] t = \dfrac{\log (50)}{1 * \log(1.085)} \\[5ex] t = \dfrac{\log (50)}{\log(1.085)} \\[5ex] t = 47.95321928 \\[3ex] t \approx 48\:years $

Top