Mathematics of Finance Applications

(1.) The table shows the performance (interest and balance) of an investment over a 5-year period.
Deborah deposits $2000 in an account that earns simple interest at an annual rate of 4.3%.
Rahab deposits $2000 in an account that earns compound interest at an annual rate of 4.3% compounded annually.
Complete the table for the 5-year period.

Year	Deborah's Annual Interest ($)	Deborah's Balance ($)	Rahab's Annual Interest ($)	Rahab's Balance ($)
1

$ P = \$2000 \\[3ex] r = 4.3\% = \dfrac{4.3}{100} = 0.043 \\[3ex] $
Year	Deborah's Annual Interest ($)	Deborah's Balance ($)	Rahab's Annual Interest ($)	Rahab's Balance ($)
1	$ 2000(0.043)(1) \\[3ex] \$86.00 $	$ 2000 + 86 \\[3ex] \$2086.00 $	$ 2000(0.043)(1) \\[3ex] \$86.00 $	$ 2000 + 86 \\[3ex] \$2086.00 $
2	$ 2000(0.043)(1) \\[3ex] \$86.00 $	$ 2086 + 86 \\[3ex] \$2172.00 $	$ 2086(0.043)(1) \\[3ex] 89.698 \\[3ex] \$89.70 $	$ 2086 + 89.698 \\[3ex] 2175.698 \\[3ex] \$2175.70 $
3	$ 2000(0.043)(1) \\[3ex] \$86.00 $	$ 2172 + 86 \\[3ex] \$2258.00 $	$ 2175.698(0.043)(1) \\[3ex] 93.555014 \\[3ex] \$93.56 $	$ 2175.698 + 93.555014 \\[3ex] 2269.253014 \\[3ex] \$2269.25 $
4	$ 2000(0.043)(1) \\[3ex] \$86.00 $	$ 2258 + 86 \\[3ex] \$2344.00 $	$ 2269.253014(0.043)(1) \\[3ex] 97.5778796 \\[3ex] \$97.58 $	$ 2269.253014 + 97.5778796 \\[3ex] 2366.830894 \\[3ex] \$2366.83 $
5	$ 2000(0.043)(1) \\[3ex] \$86.00 $	$ 2344 + 86 \\[3ex] \$2430.00 $	$ 2366.830894(0.043)(1) \\[3ex] 101.7737284 \\[3ex] \$101.77 $	$ 2366.830894 + 101.7737284 \\[3ex] 2468.604622 \\[3ex] \$2468.60 $

(2.) HSC Mathematics Standard 1 Tracy takes out a 30-year reducing balance loan of $680 000 to buy a house.
Interest is charged at 0.25% per month.
The loan is to be repaid in equal monthly instalments of $ 2866.91 over a term of 30 years.
Part of a spreadsheet used to model the reducing balance loan is shown.

Month	Amount owing at the start of the month	Interest charged for that month	Repayment	Amount owing at the end of the month
1	680 000.00	1700.00	2866.91	678 833.09
2	678 833.09

(a) Find the amount owing at the end of the second month.
(b) Suppose that the interest rate reduces to 0.15% per month and the monthly instalments remain at $2866.91
What will happen to the term of the loan?
Explain your answer without using calculations.

$ 0.25\% \\[3ex] = \dfrac{0.25}{100} \\[5ex] = 0.0025 \\[3ex] $

Month	Amount owing at the start of the month($)	Interest charged for that month($)	Repayment($)	Amount owing at the end of the month($)
1	680 000.00	$ 0.0025(680000) \\[3ex] = 1700.00 $	2866.91	$ 680000 + 1700 = 681700 \\[3ex] 681700 - 2866.91 = 678833.09 $
2	678 833.09	$ 0.0025(678833.09) \\[3ex] = 1697.082725 \\[3ex] = 1697.08 $	2866.91	$ 678833.09 + 1697.082725 = 680530.1727 \\[3ex] 680530.1727 - 2866.91 = 677663.2627 \\[3ex] $

(a.) The amount owing at the end of the second month is $677 663.26

(b.) If the interest rate is reduced to 0.15% per month while the monthly instalment is still $2866.91; then the loan will be repaid beyond 30 years.
This is because the amount owed at the end of the month will be lesser than if the interest rate was 0.25%; and because it is lesser, the loan will not be repaid sooner.

(3.) ATAR Simon has $\$5000$ that he wants to invest for a period of time without touching it.
(a) If he chooses to invest this money in an account earning compound interest at the rate of $6.5\%$, determine the:
(i) value of his investment after three years, if interest is paid annually.
(ii) time required for him to double his investment, if interest is paid monthly.

(b) Simon is currently deciding between two options and wishes to compare them.
Option A: Invest the $\$5000$ in an account earning compound interest at the rate of $5.5\%$ per annum, with interest paid monthly.

Option B: Invest the $\$5000$ in an account earning compound interest at the rate of $5.4\%$ per annum, with interest paid daily.

He decides to calculate the effective annual rate of interest for each option, in order to compare the possible investments.
He determines that Option A has an effective annual rate of interest of $5.64\%$, correct to two decimal places.
Calculate the effective annual rate of interest for Option B, correct to two decimal places, and hence decide on the better option for Simon.

$ P = \$5000 \\[3ex] (a) \\[3ex] r = 6.5\% = \dfrac{6.5}{100} = 0.065 \\[5ex] \underline{Compound\:\:Interest} \\[3ex] (i) \\[3ex] t = 3\:years \\[3ex] Annually \rightarrow m = 1 \\[3ex] A = ? \\[3ex] A = P\left(1 + \dfrac{r}{m}\right)^{mt} \\[7ex] mt = 1 * 3 = 3 \\[3ex] \dfrac{r}{m} = \dfrac{0.065}{1} = 0.065 \\[5ex] 1 + \dfrac{r}{m} = 1 + 0.065 = 1.065 \\[3ex] \left(1 + \dfrac{r}{m}\right)^{mt} = 1.065^3 = 1.207949625 \\[5ex] \rightarrow A = 5000 * 1.207949625 \\[3ex] A = 6039.748125 \\[3ex] A = \$6039.75 \\[3ex] (ii) \\[3ex] \underline{Compound\:\:Interest} \\[3ex] Investment = 5000 \\[3ex] Double\:\:Investment = 2(5000) = 10000 \\[3ex] r = 6.5\% = \dfrac{6.5}{100} = 0.065 \\[5ex] Monthly \rightarrow m = 12 \\[3ex] t = \dfrac{\log\left(\dfrac{A}{P}\right)}{m\log\left(1 + \dfrac{r}{m}\right)} \\[7ex] \dfrac{r}{m} = \dfrac{0.065}{12} = 0.005416666667 \\[5ex] 1 + \dfrac{r}{m} = 1 + 0.005416666667 = 1.0005416667 \\[3ex] \log\left(1 + \dfrac{r}{m}\right) = \log(1.0005416667) = 0.002346080197 \\[5ex] m\log\left(1 + \dfrac{r}{m}\right) = 12 * 0.002346080197 = 0.02815296237 \\[3ex] \dfrac{A}{P} = \dfrac{10000}{5000} = 2 \\[5ex] \log\left(\dfrac{A}{P}\right) = \log(2) = 0.3010299957 \\[3ex] \rightarrow t = \dfrac{0.3010299957}{0.02815296237} \\[5ex] t = 10.69265791 \\[3ex] t \approx 10.69\:years \\[3ex] (b) \\[3ex] $ Prerequisite Topic: Annual Percentage Yield (APY)

$ \underline{Option\:\:A} \\[3ex] \underline{Annual\:\:Percentage\:\:Yield} \\[3ex] APY \approx 5.64\% \\[3ex] \underline{Option\:\:B} \\[3ex] \underline{Annual\:\:Percentage\:\:Yield} \\[3ex] P = \$5000 \\[3ex] r = 5.4\% = \dfrac{5.4}{100} = 0.054 \\[3ex] Daily \rightarrow m = 365 \\[3ex] APY = \left(1 + \dfrac{r}{m}\right)^m - 1 \\[5ex] \dfrac{r}{m} = \dfrac{0.054}{365} = 0.0001479452055 \\[5ex] 1 + \dfrac{r}{m} = 1 + 0.0001479452055 = 1.000147945 \\[5ex] \left(1 + \dfrac{r}{m}\right)^m = (1.000147945)^365 = 1.055480386 \\[5ex] \rightarrow APY = 1.055480386 - 1 \\[3ex] APY = 0.05548038642 \\[3ex] APY = 5.548038642\% \\[3ex] APY \approx 5.55\% \\[3ex] 5.64\% \gt 5.55\% \\[3ex] $ Option A is better because Option A has a higher APY

(4.) NSC Selby decided today that he will save $R15\:000$ per quarter over the next four years.
He will make the first deposit into a savings account in three months' time and he will make his last deposit at the end of four years from now.

$(4.1)$ How much will Selby have at the end of four years if interest is earned at $8,8\%$ per annum, compounded quarterly?

$(4.2)$ If Selby decides to withdraw $R100\:000$ from the account at the end of three years from now, how much will he have in the amount at the end of four years from now?

Compounded quarterly means four times a year

This also means every three months

Selby will deposit that amount every three months up until four years.

The question did not indicate whether the deposit was made at the beginning or end of every three months.
So, we would assume that that deposit was made at the end of every three months.

This is a case of the Future Value of an Ordinary Annuity

$ \underline{Future\:\:Value\:\:of\:\:Ordinary\:\:Annuity} \\[3ex] PMT = R15000 \\[3ex] (4.1) \\[3ex] t = 4\:years \\[3ex] Compounded\:\:Quarterly \rightarrow m = 4 \\[3ex] r = 8.8\% = \dfrac{8.8}{100} = 0.088 \\[5ex] FV = m * PMT * \left[\dfrac{\left(1 + \dfrac{r}{m}\right)^{mt} - 1}{r}\right] \\[10ex] FV = 4 * 15000 * \left[\dfrac{\left(1 + \dfrac{0.088}{4}\right)^{4 * 4} - 1}{0.088}\right] \\[10ex] = 60000 * \left[\dfrac{\left(1 + 0.022\right)^{16} - 1}{0.088}\right] \\[7ex] = 60000 * \left[\dfrac{\left(1.022\right)^{16} - 1}{0.088}\right] \\[7ex] = 60000 * \left[\dfrac{1.41649267 - 1}{0.088}\right] \\[7ex] = 60000 * \left[\dfrac{0.41649267}{0.088}\right] \\[7ex] = \dfrac{24989.5602}{0.088} \\[5ex] = 283972.275 \\[3ex] \approx R283,972.28 \\[3ex] $ Ceteris paribus, Selby would have approximately $R283,972.28$ in his savings account at the end of four years

$(4.2)$
At the end of three years, Selby withdraws $R100,000$ at the end of three years.
How much will he have in the amount at the end of four years from now?

We can solve this question in at least two ways.
Use any method your prefer.

First Method:
First: We need to find the balance in his account at the end of three years.
Then, we subtract $R100,000$ from that balance.

Second: The amount remaining after his withdrawal (the difference) will continue to earn interest at the interest rate of $8.8\%$ compounded yearly.
It will continue to earn interest for the remaining one year. $4 - 3 = 1$
So, we shall use the Compound Interest Formula to find this amount

Third: Based on the question, we would assume that Selby continued to make the quarterly deposit of $R15,000$ for the remaining year.
That is an annuity.
So, we shall calculate the Future Value of an Annuity for that remaining one year.

Fourth: The balance in the account at the end of four years after he makes the withdrawal at the end of three years is the sum of what we get in the second and third steps.

$ (4.2) \\[3ex] First: \\[3ex] \underline{Future\:\:Value\:\:of\:\:Ordinary\:\:Annuity} \\[3ex] PMT = R15000 \\[3ex] t = 3\:years \\[3ex] m = 4 \\[3ex] r = 0.088 \\[3ex] FV = m * PMT * \left[\dfrac{\left(1 + \dfrac{r}{m}\right)^{mt} - 1}{r}\right] \\[10ex] FV = 4 * 15000 * \left[\dfrac{\left(1 + \dfrac{0.088}{4}\right)^{4 * 3} - 1}{0.088}\right] \\[10ex] = 60000 * \left[\dfrac{\left(1 + 0.022\right)^{12} - 1}{0.088}\right] \\[7ex] = 60000 * \left[\dfrac{\left(1.022\right)^{12} - 1}{0.088}\right] \\[7ex] = 60000 * \left[\dfrac{1.29840671 - 1}{0.088}\right] \\[7ex] = 60000 * \left[\dfrac{0.29840671}{0.088}\right] \\[7ex] = \dfrac{17904.4026}{0.088} \\[5ex] = R203459.12 \\[3ex] Withdrew\:\: R100000 \\[3ex] Difference = 203459.12 - 100000 = 103459.12 \\[3ex] Second: \\[3ex] \underline{Compound\:\:Interest} \\[3ex] P = 103459.12 \\[3ex] t = 1\:year \\[3ex] r = 0.088 \\[3ex] m = 4 \\[3ex] A = P\left(1 + \dfrac{r}{m}\right)^{mt} \\[7ex] A = 103459.12\left(1 + \dfrac{0.088}{4}\right)^{4 * 1} \\[7ex] = 103459.12\left(1 + 0.022\right)^{4} \\[7ex] = 103459.12 * (1.022)^4 \\[3ex] = 103459.12 * 1.09094683 \\[3ex] = 112868.399 \\[3ex] Third: \\[3ex] \underline{Future\:\:Value\:\:of\:\:Ordinary\:\:Annuity} \\[3ex] PMT = 15000 \\[3ex] t = 1\:years \\[3ex] m = 4 \\[3ex] r = 0.088 \\[3ex] FV = m * PMT * \left[\dfrac{\left(1 + \dfrac{r}{m}\right)^{mt} - 1}{r}\right] \\[10ex] FV = 4 * 15000 * \left[\dfrac{\left(1 + \dfrac{0.088}{4}\right)^{4 * 1} - 1}{0.088}\right] \\[10ex] = 60000 * \left[\dfrac{\left(1 + 0.022\right)^{4} - 1}{0.088}\right] \\[7ex] = 60000 * \left[\dfrac{\left(1.022\right)^{4} - 1}{0.088}\right] \\[7ex] = 60000 * \left[\dfrac{1.09094683 - 1}{0.088}\right] \\[7ex] = 60000 * \left[\dfrac{0.09094683}{0.088}\right] \\[7ex] = \dfrac{5456.8098}{0.088} \\[5ex] = 62009.2023 \\[3ex] Fourth: \\[3ex] Balance = 112868.399 + 62009.2023 \\[3ex] = 174877.601 \\[3ex] \approx R174877.60 \\[3ex] $ Second Method:
First: Selby decides to withdraw $100000$ at the end of three years.
That withdrawal would have earned interest compounded annually at the interest rate of $8.8\%$.
We shall calculate use the Compound Interest formula and calculate that amount.

Second: We shall subtract that compound amount from what should have been in his account at the end of four years had he not made that withdrawal.
In other words, we shall calculate the difference between the future value of the ordinary annuity at the end of four years and the compound amount of the withdrawal at the end of three years

$ First: \\[3ex] \underline{Compound\:\:Interest} \\[3ex] P = 100000 \\[3ex] t = 1\:year \\[3ex] r = 0.088 \\[3ex] m = 4 \\[3ex] A = P\left(1 + \dfrac{r}{m}\right)^{mt} \\[7ex] A = 100000\left(1 + \dfrac{0.088}{4}\right)^{4 * 1} \\[7ex] = 100000\left(1 + 0.022\right)^{4} \\[7ex] = 100000 * (1.022)^4 \\[3ex] = 100000 * 1.09094683 \\[3ex] = 109094.683 \\[3ex] Second: \\[3ex] Balance = 283972.275 - 109094.683 \\[3ex] = 174877.592 \\[3ex] \approx R174877.59 \\[3ex] $ Ceteris paribus, Selby would have approximately $R174877.60$ in his savings account at the end of four years after he withdrawing $R100,000$ at the end of three years from the account.

(5.) Someone wants to set aside $\$500$ in a savings account at the beginning of each month for ten years.
The person intends to invest this fund in a financial institution that gives an interest rate of $5.5\%$ per year.
How much is the balance in the account at the end?

If the question does not state that the interest is simple interest, then assume compound interest.

This is a case of Annuity Due because the payments are made at the beginning of each month.

The interest is compounded monthly because the fund is deposited each month.

$ \underline{Future\:\:Value\:\:of\:\:Annuity\:\:Due} \\[3ex] PMT = \$500 \\[3ex] r = 5.5\% = \dfrac{5.5}{100} = 0.055 \\[5ex] t = 10\:years \\[3ex] Compounded\:\:monthly\rightarrow m = 12 \\[3ex] FV = ? \\[3ex] FV = m * PMT * \left[\dfrac{\left(1 + \dfrac{r}{m}\right)^{mt} - 1}{r}\right] * \left(1 + \dfrac{r}{m}\right) \\[10ex] FV = 12 * 500 * \left[\dfrac{\left(1 + \dfrac{0.055}{12}\right)^{12 * 10} - 1}{0.055}\right] * \left(1 + \dfrac{0.055}{12}\right) \\[10ex] = 6000 * \left[\dfrac{\left(1 + 0.00458333333\right)^{120} - 1}{0.055}\right] * \left(1 + 0.00458333333\right) \\[7ex] = 6000 * \left[\dfrac{\left(1.00458333\right)^{120} - 1}{0.055}\right] * \left(1.00458333\right) \\[7ex] = 6000 * \left[\dfrac{\left(1.00458333\right)^{120} - 1}{0.055}\right] * \left(1.00458333\right) \\[7ex] = 6027.49998 * \left[\dfrac{1.73107573 - 1}{0.055}\right] \\[5ex] = 6027.49998 * \left[\dfrac{0.73107573}{0.055}\right] \\[5ex] = \dfrac{4406.55895}{0.055} \\[5ex] = 80119.2536 \\[3ex] \approx \$80119.26 \\[3ex] $ Ceteris paribus, the balance in the account at the end of ten years would be about $\$80,119.26$

(6.) Most people do not have the choice to drive or fly to a destination close to home but perhaps we will in the future.
Two companies, one in Massachusetts and one in Slovakia, are working on producing a flying car.
A prototype has entered the testing phase in Slovakia and the Massachusetts company is working on perfecting retractable wings on their car model.
Although mass production has not begun, the prototypes have successfully reached lift off with ranges of just over 400 miles and speeds just over 100 miles per hour.
(Source: Marquis, E. "Aeromobil 2.5 flying car makes first flight test." AolAutos. 25 Oct 2013. Retrieved from http://translogic.aolautos.com/2013/10/25/aeromobil-2-5-flying-car-makes-first-test-flight/)
Suppose the sticker price on a particular car was $17,090.
A consumer expects to qualify for a rebate of $4,500 and receive an additional $3,500 for trading in his current car.
Six years ago the consumer invested $7,500 in a savings account earning 2% APR compounded monthly.
(a.) How much would the consumer have saved to purchase the car?
(b.) Ignoring taxes, what is the difference between the price of the car and the amount saved to purchase the car?

(a.) Amount saved to purchase the car

$ P = \$7500 \\[3ex] r = 2\% = \dfrac{2}{100} = 0.02 \\[5ex] m = 12 \\[3ex] t = 6\;years \\[3ex] A = P\left(1 + \dfrac{r}{m}\right)^{mt} \\[5ex] = 7500\left(1 + \dfrac{0.02}{12}\right)^{12 * 6} \\[5ex] = 7500(1 + 0.0016666667)^{72} \\[3ex] = 7500(1.0016666667)^{72} \\[3ex] = 7500(1.127384233) \\[3ex] = 8455.381745 \\[3ex] \approx \$8455.38 \\[3ex] $ Price of the car

$ Sticker\;\;price = \$17090 \\[3ex] Rebate = \$4500 \\[3ex] Trade-in\;\;value\;\;of\;\;old\;\;car = \$3500 \\[3ex] Price = 17090 - 4500 - 3500 = \$9090 \\[3ex] $ (b.) Difference between the price of the car and the amount saved to purchase the car

$ 9090 - 8455.381745 \\[3ex] = 634.618255 \\[3ex] \approx \$634.62 $

(7.) A couple has $\$25,000$ in their retirement savings today.
How many years do they have to save at $6\%$, putting in $\$1,000$ at the beginning of each year, to achieve $\$80,000?$

If the question does not state that the interest is simple interest, then assume compound interest.

First: This is a case of Compound Interest because their retirement savings of $\$25,000$ earns interest compounded annually/yearly at the interest rate of $6\%$.

Second: This is also a case of Annuity Due because the couple would have to deposit $\$1,000$ at the beginning of each year.

$ \underline{Compound\:\:Interest\:\:and\:\:Annuity\:\:Due} \\[3ex] P = \$25000 \\[3ex] r = 6\% = \dfrac{6}{100} = 0.06 \\[5ex] PMT = \$1000 \\[3ex] CFV = \$80000 \\[3ex] Compounded\:\:annually \rightarrow m = 1 \\[3ex] t = ? \\[3ex] t = \dfrac{\log\left[\dfrac{rCFV + PMT(m + r)}{rP + PMT(m + r)}\right]}{m\log\left(1 + \dfrac{r}{m}\right)} \\[10ex] = \dfrac{\log\left[\dfrac{0.06(80000) + 1000(1 + 0.06)}{0.06(25000) + 1000(1 + 0.06)}\right]}{1 * \log\left(1 + \dfrac{0.06}{1}\right)} \\[10ex] = \dfrac{\log\left[\dfrac{4800 + 1000(1.06)}{1500 + 1000(1.06)}\right]}{1 * \log\left(1 + 0.06\right)} \\[10ex] = \dfrac{\log\left[\dfrac{4800 + 1060}{1500 + 1060}\right]}{\log\left(1.06\right)} \\[7ex] = \dfrac{\log\left[\dfrac{5860}{2560}\right]}{\log\left(1.06\right)} \\[7ex] = \dfrac{\log(2.2890625)}{0.0253058653} \\[5ex] = \dfrac{0.359657651}{0.0253058653} \\[5ex] = 14.2124226\:years \\[3ex] Let\:\:us\:\:check\:\:to\:\:confirm \\[3ex] \underline{Check} \\[3ex] \underline{Compound\:\:Interest} \\[5ex] P = \$25000 \\[3ex] r = 0.06 \\[3ex] m = 1 \\[3ex] t = 14.2124226\:years \\[3ex] A = P\left(1 + \dfrac{r}{m}\right)^{mt} \\[7ex] = 25000\left(1 + \dfrac{0.06}{1}\right)^{1(14.2124226)} \\[7ex] = 25000\left(1 + 0.06\right)^{14.2124226} \\[7ex] = 25000(1.06)^{14.2124226} \\[5ex] = 25000(2.2890625) \\[3ex] = \$57226.5625 \\[3ex] \underline{Annuity\:\:Due} \\[3ex] PMT = \$1000 \\[3ex] r = 0.06 \\[3ex] m = 1 \\[3ex] t = 14.2124226\:years \\[3ex] FV = m * PMT * \left[\dfrac{\left(1 + \dfrac{r}{m}\right)^{mt} - 1}{r}\right] * \left(1 + \dfrac{r}{m}\right) \\[10ex] = 1 * 1000 * \left[\dfrac{\left(1 + \dfrac{0.06}{1}\right)^{1(14.2124226)} - 1}{0.06}\right] * \left(1 + \dfrac{0.06}{1}\right) \\[10ex] = 1000 * \left[\dfrac{\left(1 + 0.06\right)^{14.2124226} - 1}{0.06}\right] * \left(1 + 0.06\right) \\[10ex] = 1000 * \left[\dfrac{\left(1.06\right)^{14.2124226} - 1}{0.06}\right] * \left(1.06\right) \\[10ex] = 1000 * 1.06 * \left[\dfrac{2.2890625 - 1}{0.06}\right] \\[7ex] = 1060 * \left[\dfrac{1.2890625}{0.06}\right] \\[7ex] = \dfrac{1060 * 1.2890625}{0.06} \\[5ex] = \dfrac{1366.40625}{0.06} \\[5ex] = \$22773.4375 \\[5ex] \underline{Combined\:\:Amount} \\[3ex] CFV = 57226.5625 + 22773.4375 = \$80000 $

(8.) Titus wants to accumulate $125,000 for retirement in 30 years.
He has two choices.
Plan A is a single deposit into an account with annual compounding and an APR of 4%.
Plan B is a single deposit into an account with continuous compounding and an APR of 3.5%.
How much does he need to deposit in each account in order to reach the goal?

Plan A is a case of Compound Interest
Plan B is a case of Continuous Compound Interest.

$ A = \$125000 \\[3ex] t = 30\;years \\[5ex] \underline{Plan\;A} \\[3ex] Annual\;\;compounding \implies m = 1 \\[3ex] r = 4\% = \dfrac{4}{100} = 0.04 \\[5ex] P = ? \\[5ex] P = \dfrac{A}{\left(1 + \dfrac{r}{m}\right)^{mt}} \\[5ex] = \dfrac{125000}{\left(1 + \dfrac{0.04}{1}\right)^{1(30)}} \\[5ex] = \dfrac{125000}{(1 + 0.04)^{30}} \\[5ex] = \dfrac{125000}{(1.04)^{30}} \\[5ex] = \dfrac{125000}{3.24339751} \\[5ex] = 38539.8335 \\[3ex] \approx \$38539.83 \\[3ex] $ Titus needs to deposit $38539.83 in Plan A in order to accumulate $125000 for retirement in 30 years.

$ \underline{Plan\;B} \\[3ex] r = 3.5\% = \dfrac{3.5}{100} = 0.035 \\[5ex] P = \dfrac{A}{e^{rt}} \\[5ex] = \dfrac{125000}{e^{0.035(30)}} \\[5ex] = \dfrac{125000}{e^{1.05}} \\[5ex] = \dfrac{125000}{2.718281828} \\[5ex] = 45984.93015 \\[3ex] \approx \$45,984.93 \\[3ex] $ Titus needs to deposit $45984.93 in Plan B in order to accumulate $125000 for retirement in 30 years.

(9.) NSC Tshepo takes out a home loan over $20$ years to buy a house that costs $R1\:500\:000$.

$(9.1)$ Calculate the monthly installment if interest is charged at $10,5\%$ p.a, compounded monthly.

$(9.2)$ Calculate the outstanding balance immediately after the $144^{th}$ payment was made.

$ \underline{Amortization} \\[3ex] PV = R1500000 \\[3ex] t = 20\:years \\[3ex] r = 10.5\% = \dfrac{10.5}{100} = 0.105 \\[5ex] Compounded\:\:monthly \rightarrow m = 12 \\[3ex] PMT = ? \\[3ex] (9.1) \\[3ex] PMT = \dfrac{PV}{m} * \left[\dfrac{r}{1 - \left(1 + \dfrac{r}{m}\right)^{-mt}}\right] \\[10ex] PMT = \dfrac{1500000}{12} * \left[\dfrac{0.105}{1 - \left(1 + \dfrac{0.105}{12}\right)^{-1 * 12 * 20}}\right] \\[10ex] = 125000 * \left[\dfrac{0.105}{1 - \left(1 + 0.00875\right)^{-240}}\right] \\[7ex] = 125000 * \left[\dfrac{0.105}{1 - \left(1.00875\right)^{-240}}\right] \\[7ex] = 125000 * \left[\dfrac{0.105}{1 - 0.123580101}\right] \\[5ex] = 125000 * \left[\dfrac{0.105}{0.876419899}\right] \\[5ex] = \dfrac{125000 * 0.105}{0.876419899} \\[5ex] = \dfrac{13125}{0.876419899} \\[5ex] = 14975.6983 \\[3ex] \approx R14,975.70 \\[3ex] (9.2) \\[3ex] 12\:months = 1\:year \\[3ex] 144th\:\:payment \rightarrow \dfrac{144}{12} = 12th\:year\:\:payment \\[5ex] Remaining = 20 - 12 = 8\:years \\[3ex] $ Ask your students how they will calculate the outstanding balance after the $144^{th}$ payment.
Note their responses.
Some of the responses may include:
Find the total payment...for 20 years ...which is 240 months
Find the payment for 144 months
Subtract that payment from the total payment
...among other responses.

Remind them that these are Mortgage payments...Fixed Rate Mortgage
Show them how it works...using the example on my website
You can also use the Loan Amortization Calculator to confirm the calculations
Any monthly payment made is used to offset the interest earned during that period...first step
Then, any remaining balance is applied toward the principal.
The same principle applies to car payments and other amortized payments.

We can find the outstanding balance at the end of the $144th$ payemnt (at the end of $12$ years) in at least two ways.
Use any method you prefer.

First Method: Find the present value of the ordinary annuity for the remaining $8$ years.
OR
Second Method:
Compare to the previous response of "probably" one of your students.
But, explain the concept well for your students to understand.

Use the Compound Interest formula to calculate the future value of the loan amount for $12$ years.

Remember that the monthly payment of $14975.70$ was found using the Amortization formula for the entire term of the loan.

So, use the Future Value of an Ordinary Annuity formula and calculate the future value of that payment for $12$ years.
Then, subtract the future value of that payment from the future value of the loan amount.

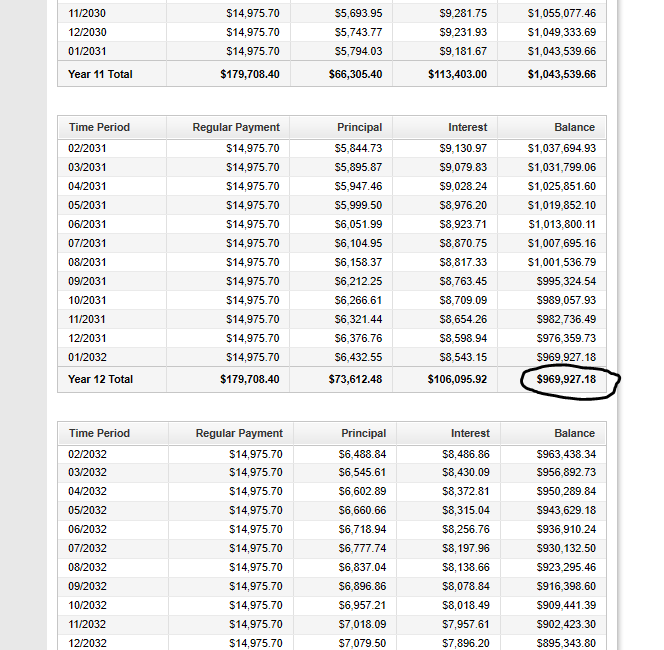
$ \underline{First\:\:Method} \\[3ex] \underline{Present\:\:Value\:\:of\:\:Ordinary\:\:Annuity} \\[3ex] t = 8\:years \\[3ex] PMT = R14975.6983 \\[3ex] r = 0.105 \\[3ex] m = 12 \\[3ex] PV = m * PMT * \left[\dfrac{1 - \left(1 + \dfrac{r}{m}\right)^{-mt}}{r}\right] \\[10ex] PV = 12 * 14975.6983 * \left[\dfrac{1 - \left(1 + \dfrac{0.105}{12}\right)^{-1 * 12 * 8}}{0.105}\right] \\[10ex] = 179708.38 * \left[\dfrac{1 - \left(1 + 0.00875\right)^{-96}}{0.105}\right] \\[7ex] = 179708.38 * \left[\dfrac{1 - \left(1.00875\right)^{-96}}{0.105}\right] \\[7ex] = 179708.38 * \left[\dfrac{1 - 0.43329075}{0.105}\right] \\[5ex] = 179708.38 * \left[\dfrac{0.56670925}{0.105}\right] \\[5ex] = \dfrac{179708.38 * 0.56670925}{0.105} \\[5ex] = \dfrac{101842.401}{0.105} \\[5ex] = 969927.629 \\[3ex] \approx R969,927.63 \\[3ex] \underline{Second\:\:Method} \\[3ex] \underline{Compound\:\:Interest\:\:and\:\:Future\:\:Value\:\:of\:\:Ordinary\:\:Annuity} \\[3ex] \underline{Compound\:\:Interest} \\[3ex] P = R1500000 \\[3ex] r = 0.105 \\[3ex] t = 12\:years \\[3ex] m = 12 \\[3ex] A = P\left(1 + \dfrac{r}{m}\right)^{mt} \\[7ex] A = 1500000\left(1 + \dfrac{0.105}{12}\right)^{12 * 12} \\[7ex] = 1500000\left(1 + 0.00875\right)^{144} \\[7ex] = 1500000\left(1.00875\right)^{144} \\[7ex] = 1500000(3.50615308) \\[3ex] = R5259229.62 \\[3ex] \underline{Future\:\:Value\:\:of\:\:Ordinary\:\:Annuity} \\[3ex] m = 12 \\[3ex] PMT = R14975.6983 \\[3ex] r = 0.105 \\[3ex] t = 12\:years \\[3ex] FV = m * PMT * \left[\dfrac{\left(1 + \dfrac{r}{m}\right)^{mt} - 1}{r}\right] \\[10ex] FV = 12 * 14975.6983 * \left[\dfrac{\left(1 + \dfrac{0.105}{12}\right)^{12 * 12} - 1}{0.105}\right] \\[10ex] = 179708.38 * \left[\dfrac{\left(1 + 0.00875\right)^{144} - 1}{0.105}\right] \\[7ex] = 179708.38 * \left[\dfrac{\left(1.00875\right)^{144} - 1}{0.105}\right] \\[7ex] = 179708.38 * \left[\dfrac{3.50615308 - 1}{0.105}\right] \\[5ex] = 179708.38 * \left[\dfrac{2.50615308}{0.105}\right] \\[5ex] = \dfrac{179708.38 * 2.50615308}{0.105} \\[5ex] = \dfrac{450376.71}{0.105} \\[5ex] = R4289302 \\[3ex] \underline{Balance\:\:after\:\:144th\:\:payment} \\[3ex] Balance = 5259229.62 - 4289302 = R969,927.62 \\[3ex] $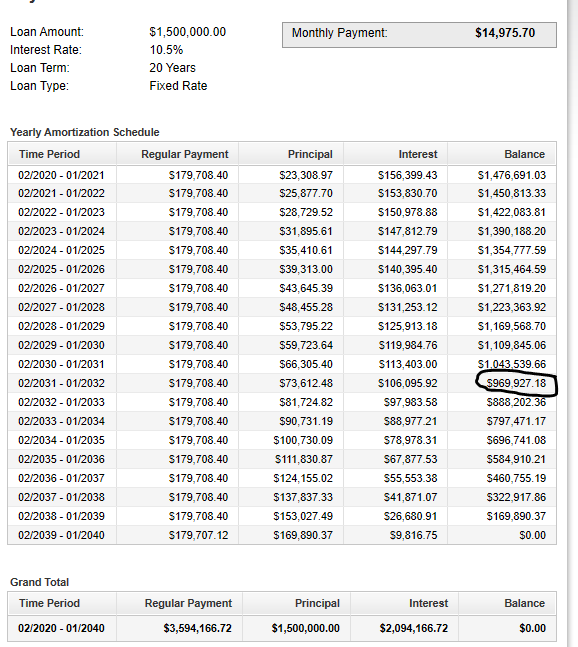 Number 9: Part 1

(10.) HSC Mathematics Standard 1 James invests $5000 per annum simple interest for 2 years, while Sally invests $5000 at 3% per annum compounded annually for 2 years.
For the given investments, which of the following statements is TRUE?
A.   James earns more interest than Sally.
B.   Sally earns more interest than James.
C.   James and Sally earn the same amount of interest.
D.   There is not enough information to compare the interest earned by James and Sally.

For one year, James and Sally will earn the same interest.
However, for two years?
Well, it's evident Sally will earn more interest because it is compounded annually for anything time beyond one year.
Let us show it.

$ \underline{James:\;\;Simple\;\;Interest} \\[3ex] P = \$5000 \\[3ex] r = 3\% = \dfrac{3}{100} = 0.03 \\[5ex] t = 2\;years \\[3ex] SI = Prt \\[3ex] = 5000(0.03)(2) \\[3ex] = 300 \\[3ex] = \$300.00 \\[3ex] \underline{Sally:\;\;Compound\;\;Interest} \\[3ex] compounded\;\;annually \\[3ex] P = \$5000 \\[3ex] r = 3\% = \dfrac{3}{100} = 0.03 \\[5ex] t = 2\;years \\[3ex] m = 1 \\[3ex] CI = P\left(1 + \dfrac{r}{m}\right)^{mt} - P \\[5ex] = 5000 * \left(1 + \dfrac{0.03}{1}\right)^{1 * 2} - 5000 \\[5ex] = 5000(1 + 0.03)^2 - 5000 \\[3ex] = 5000(1.03)^2 - 5000 \\[3ex] = 5000(1.0609) - 5000 \\[3ex] = 5304.5 - 5000 \\[3ex] = 304.5 \\[3ex] \approx \$304.50 \\[3ex] $ Because $\$304.50$ is greater than $\$300.00$, Sally earns more interest than James.

Student: Mr. C, you mentioned earlier that if the time was 1 year, then the simple interest would be equal to the compound interest.
Teacher: If the compound interest was compounded annually...yes
And if the principal and interest rate was the same for both the simple interest and the compound interest
Student: Okay, can you give an example?
Teacher: With numbers, or without numbers, or both?
Student: Both...
Teacher: Let's assume a time of 1 year for the question, rather than 2 years

$ P = \$5000 \\[3ex] r = 0.03 \\[3ex] t = 1\;year \\[3ex] \underline{Simple\;\;Interest} \\[3ex] SI = Prt \\[3ex] = 5000(0.03)(1) \\[3ex] = 150 \\[3ex] = \$150.00 \\[5ex] \underline{Compound\;\;Interest} \\[3ex] compounded\;\;annually \implies m = 1 \\[3ex] A = P\left(1 + \dfrac{r}{m}\right)^{mt} \\[5ex] = 5000 * \left(1 + \dfrac{0.03}{1}\right)^{1 * 1} \\[5ex] = 5000 * (1 + 0.03)^1 \\[3ex] = 5000(1.03) \\[3ex] = 5150 \\[3ex] CI = A - P \\[3ex] = 5150 - 5000 \\[3ex] = 150 \\[3ex] = \$150.00 \\[3ex] $ Both interests (simple interest and compound interest) are the same.
Here is the example of doing the calculations without numbers

(11.) A couple wants to save for a down payment on a car.
They think they need $\$100,000$ in five years.
If the interest rate is $4\%$ and they start at the end of the year when they both get bonuses from their employers, what do they to put aside annually?

If the question does not state that the interest is simple interest, then assume compound interest.

If the question does not state the number of compounded periods per year for which the interest is compounded, then assume that the interest is compounded annually.

$ \underline{Sinking\:\:Fund} \\[3ex] FV = \$100000 \\[3ex] t = 5\:years \\[3ex] r = 4\% = \dfrac{4}{100} = 0.04 \\[5ex] PMT = ? \\[3ex] Compounded\:\:annually\rightarrow m = 1 \\[3ex] PMT = \dfrac{r * FV}{m * \left[\left(1 + \dfrac{r}{m}\right)^{mt} - 1\right]} \\[10ex] = \dfrac{0.04 * 100000}{1 * \left[\left(1 + \dfrac{0.04}{1}\right)^{1 * 5} - 1\right]} \\[10ex] = \dfrac{4000}{1 * \left[(1 + 0.04)^{5} - 1\right]} \\[5ex] = \dfrac{4000}{1 * \left[(1.04)^{5} - 1\right]} \\[5ex] = \dfrac{4000}{1 * \left[1.2166529 - 1\right]} \\[5ex] = \dfrac{4000}{0.2166529} \\[5ex] = 18462.7116 \\[3ex] \approx \$18462.71 \\[3ex] $ The couple needs to set aside about $\$18,462.71$ annually

(12.) ACT A formula to estimate the monthly payment, p dollars, on a short-term loan is $$ p = \dfrac{\dfrac{1}{2}ary + a}{12y} $$ where a dollars is the amount of the loan, r is the annual interest rate expressed as a decimal, and y years is the length of the loan.
When a is multiplied by 2, what is the effect on p?
A. p is divided by 6
B. p is divided by 2
C. p does not change
D. p is multiplied by 2
E. p is multiplied by 4

$ p = \dfrac{\dfrac{1}{2}ary + a}{12y} \\[7ex] when\;\;a\;\;is\;\;multiplied\;\;by\;\;2 \implies a = 2a \\[3ex] p = \dfrac{\dfrac{1}{2}2ary + 2a}{12y} \\[7ex] p = \dfrac{2\left(\dfrac{1}{2}ary + a\right)}{12y} \\[7ex] p = \dfrac{\dfrac{1}{2}ary + a}{6y}...eqn.(1) \\[7ex] 2p = 2 * \dfrac{\dfrac{1}{2}ary + a}{12y} = \dfrac{\dfrac{1}{2}ary + a}{6y}...eqn.(2) \\[7ex] eqn.(1) = eqn.(2) \\[3ex] \implies \\[3ex] $ p is multiplied by 2

(14.) Several factors are considered by lenders when reviewing credit applications.
One item is a FICO score which ranges in point value from 300 to 850.
While your FICO score is only one component in the decision making process, a score of mid seven hundred and higher is typically deemed as 'A' credit and can gleam the best interest rate offered at the time.
The below chart shows a partial listing and the associated approximations of the percentages of the US population that fell into the given ranges of FICO scores in recent years.

Population in %	Credit score range	Rating
13	800 – 850	Excellent
27	750 – 799	Above Average
18	700 – 749	Average
15	650 – 699	Below Average
12	600 – 649	Poor

Data correlated from over 70,000 consumers pointed to an average FICO credit score of 664 at the time that the above chart was calculated.
(Source: My FICO. Sept 2013. Retrieved from www.myfico.com.)

According to the above chart, how many points must be realized to increase the cited data average FICO credit score to an excellent rating?

A. 36 B. 64
C. 86 D. 136

Excellent rating credit score range = 800 – 850
Minimum credit score for Excellent rating = 800
Points to get from 664 to 800
= 800 − 664
= 136

(18.) Decide whether these statements make sense (or is clearly true) or does not make sense (or is clearly false).
Explain your reasoning.

(I.) Both banks were paying the same annual percentage rate (APR), but one had a higher annual percentage yield than the other (APY).

(II.) My bank paid an annual interest rate (APR) of 3.0% but at the end of the year my account balance had grown by 3.1%.

(III.) Bank A was offering simple interest at 4.25% per year, which was clearly a better deal than the 4.25% compound interest rate at Bank B.

(IV.) The bank that pays the highest annual percentage rate (APR) is always the best, no matter how often the interest is compounded.

(I.) This statement makes sense because the banks can have a different number of compounding periods, which results in different annual percentage yields.

(II.) This makes sense, because the annual interest rate (APR) does not always match the annual percentage yield (APY).

(III.) The statement does not make sense, because the compound interest pays more than the simple interest.

(IV.) The statement does not make sense because, depending on how often the interest is compounded, a lower APR could result in a higher annual percentage yield.

(20.) Consider two investments, one earning simple interest and one earning compound interest.
If both start with the same initial deposit (and you make no other deposits or withdrawals) and earn the same annual interest rate, how will the balance in the simple interest account compare to that of the compound interest?
Choose the correct answer below.

A. The account with simple interest will have the same balance as the account with compound interest because the initial deposits are equal.

B. The account with simple interest will have a smaller balance than the account with compound interest because the more times interest is applied to an investment, the smaller the balance.

C. The account with simple interest will have a smaller balance than the account with compound interest because compound interest is interest paid both on the original investment and on all interest that has been added to the original investment.

D. The account with simple interest will have a greater balance than the account with compound interest because compound interest is interest paid only on the original investment.

E. The account with simple interest will have the same balance as the account with compound interest because the annual interest rates are equal.

C. The account with simple interest will have a smaller balance than the account with compound interest because compound interest is interest paid both on the original investment and on all interest that has been added to the original investment.

(22.) What is continuous compounding? How does the APY for continuous compounding compare to the APY for, say, daily compounding?
Explain the formula for continuous compounding.

A. Compounding at least once per year is called continuous compounding.
The APY for continuous compounding is smaller than the APY for daily compounding.
The formula for continuous compounding is also known as the compound interest formula.

B. Compounding infinitely many times per year is called continuous compounding.
The APY for continuous compounding is only slightly larger than the APY for daily compounding.
The formula for continuous compounding is a special form of the compound interest formula.

C. Compounding twice daily is called continuous compounding.
The APY for continuous compounding is only slightly larger than the APY for daily compounding.
The formula for continuous compounding is a special form of the simple interest formula.

D. Compounding daily is also known as continuous compounding.
The APY for continuous compounding is equivalent to the APY for daily compounding.
The formula for continuous compounding is also known as the compound interest formula.

B. Compounding infinitely many times per year is called continuous compounding.
The APY for continuous compounding is only slightly larger than the APY for daily compounding.
The formula for continuous compounding is a special form of the compound interest formula.

(24.) Explain why the term APR/n appears in the compound interest formula for interest paid n times a year.

A. APR represents the annual percentage rate (as a decimal).
Since the APR represents a yearlong rate, to account for fluctuation, the rate needs to be divided by the number of compounding periods per year, n.

B. APR represents the annual percentage rate (as a decimal).
To account for the interest paid n times a year, this annual (yearly) rate needs to be divided by the number of compounding periods per year, n.

C. APR represents the annual principle rate.
Since the APR is the total amount of interest earned in a year, it needs to be divided by the number of compounding periods per year, n.

D. APR represents the annual principle rate.
The APR represents the original investment and must be divided by the number of compounding periods per year, n, in order to determine the yearly compounded interest rate.

B. APR represents the annual percentage rate (as a decimal).
To account for the interest paid n times a year, this annual (yearly) rate needs to be divided by the number of compounding periods per year, n.

(26.) Suppose you use the compound interest formula to calculate how much you must deposit into a college fund today if you want it to grow in value to $30,000 in ten years.
What does the calculation assume?

A. The fund has continuous compounding because it is not clearly stated in the given situation.

B. The fund earns simple interest rather than compound interest because no such formula exists to predict the growth of investments that use compound interest.

C. The fund earns simple interest rather than compound interest because compound interest rates cannot be predicted with any certainty.

D. The fund has continuous compounding because the formula is invalid for simple interest.

E. The calculation assumes that the average APR remains constant for ten years because it is extremely difficult to find investments with a constant interest rate.

F. The calculation assumes that the average APR remains constant for ten years because the formula does not use APR when calculating this value.

E. The calculation assumes that the average APR remains constant for ten years because it is extremely difficult to find investments with a constant interest rate.

(28.) What is the difference between simple interest and compound interest?
Why do you end up with more money with compound interest?

A. Simple interest is interest paid at a fixed rate over time whereas compound interest fluctuates over time.
Since the rates for compound interest are always increasing, it results in a larger amount of money over time compared to simple interest.

B. Simple interest is interest paid only on 50% of the original investment whereas compound interest is interest paid only on 100% of the original investment.
Since compound interest is calculated based on a larger amount than simple interest, it results in a larger amount of money over time.

C. Simple interest is interest paid only on the original investment whereas compound interest is interest paid both on the original investment and on all interest that has been added to the original investment.
Since compound interest is calculated based on a larger amount than simple interest, it results in a larger amount of money over time.

D. Simple interest is interest paid both on the original investment and on all interest that has been added to the original investment whereas compound interest is interest paid only on the original investment.
Since compound interest is calculated based on a smaller amount, it results in a larger amount of money over time.

C. Simple interest is interest paid only on the original investment whereas compound interest is interest paid both on the original investment and on all interest that has been added to the original investment.
Since compound interest is calculated based on a larger amount than simple interest, it results in a larger amount of money over time.

(29.) Explore continuous compounding by answering these questions.

(a.) For an APR of 12%, make a table that displays the APY for n = 4, 12, 365, 500, and 1000.
Complete the following table.

Annual Yield (APY) for APR = 12% with Various Numbers of Compounding Periods (m)
m	1	4	12	365	500	1000
APY	12%	............	............	............	............	............

Round to two decimal places as needed.

(b.) Find the APY for continuous compounding at an APR of 12%.

(c.) Choose the correct graph below.

Number 29

(d.) In words, compare the APY with continuous compounding to the APY with other types of compounding.

You deposit $300 in an account with an APR of 12%.
With continuous compounding, how much money will you have:
(e.) At the end of 1 year?
(f.) At the end of 5 years?

(a.) Let us do this question using the TI-84 technology to make the calculation faster

$ APY = \left(1 + \dfrac{r}{m}\right)^m - 1 \\[5ex] r = APR = 12\% = 0.12...this\;\;is\;\;a\;\;constant\;\;for\;\;this\;\;question \\[3ex] L_1 = 1, 4, 12, 365, 500, 1000 \\[3ex] L_2 = \dfrac{r}{m} = \dfrac{0.12}{L_1} \\[5ex] L_3 = 1 + \dfrac{r}{m} = 1 + L_2 \\[5ex] L_4 = \left(1 + \dfrac{r}{m}\right)^m = L_3 ^{L_1} \\[5ex] L_5 = APY = \left(1 + \dfrac{r}{m}\right)^m - 1 = L_4 - 1 \\[5ex] L_6 = APY\;\;in\;\;\% = L_5 * 100 \\[3ex] $ Number 29-1st

$ 12\% \\[3ex] 12.550881\% \approx 12.55\% \\[3ex] 12.6825030132\% \approx 12.68\% \\[3ex] 12.74746156435\% \approx 12.75\% \\[3ex] 12.74806183389\% \approx 12.75\% \\[3ex] 12.74887342806\% \approx 12.75\% \\[3ex] $ The completed table is:

Annual Yield (APY) for APR = 12% with Various Numbers of Compounding Periods (m)
m	1	4	12	365	500	1000
APY	12%	12.55%	12.68%	12.75%	12.75%	12.75%

$ (b.) \\[3ex] APY = e^r - 1 \\[3ex] = e^{0.12} - 1 \\[3ex] = 0.1274968516 \\[3ex] = 12.74968516\% \\[3ex] \approx 12.75\% \\[5ex] $ (c.) The APY keeps increasing until it approximately remains at constant (appears to flatten) at 12.75%
Hence, the correct graph is:

Number 29-2nd

(d.) The APY is higher with continuous compounding than with any other compounding.
As the number of compoundings per year increases, the APY gets closer to the APY obtained with continuous compounding.

$ A = Pe^{rt} \\[3ex] P = \$300 \\[3ex] r = 12\% = 0.12 \\[3ex] (e.) \\[3ex] t = 1\;year \\[3ex] A = 300 * e^{0.12 * 1} \\[4ex] A = 338.2490555 \\[3ex] A \approx \$338.25 \\[5ex] (f.) \\[3ex] t = 5\;years \\[3ex] A = 300 * e^{0.12 * 5} \\[4ex] A = 546.6356401 \\[3ex] A \approx \$546.64 $