Solved Examples: Present Value of Ordinary Annuity and Amortization

Samuel Dominic Chukwuemeka (SamDom For Peace)

As applicable:
Formulas Used: Mathematics of Finance

Verify Loan Amortization Table with: Loan Amortization Table Calculator from Capital Bank (https://www.capitalbank.com/calculators/mortgage-calculator)

NOTE: Unless instructed otherwise;
For all financial calculations, do not round until the final answer.
Do not round intermediate calculations. If it is too long, write it to "at least" $5$ decimal places.
Round your final answer to $2$ decimal places.
Make sure you include your unit.

Solve all questions.
Use at least two methods where applicable.
Write the name of any formulas that you use.
Show all work.

For NSC Students
For the Questions:
Any space included in a number indicates a comma used to separate digits...separating multiples of three digits from behind.
Any comma included in a number indicates a decimal point.
For the Solutions:
Decimals are used appropriately rather than commas
Commas are used to separate digits appropriately.

(1.) Peter purchased a car.
The car is going to be financed for $10,000 for 48 months at an APR (Annual Percentage Rate) of 7%.
(a.) Calculate the monthly payments on the loan.
(b.) What is the total interest?

This is a case of Amortization

$ \underline{Amortization} \\[3ex] PV = \$10000 \\[3ex] t = 48\:months = \dfrac{48}{12}\:years = 4\: years \\[5ex] r = 7\% = \dfrac{7}{100} = 0.07 \\[5ex] Compounded\:\:monthly \rightarrow m = 12 \\[3ex] PMT = ? \\[3ex] (a.) \\[3ex] PMT = \dfrac{PV}{m} * \left[\dfrac{r}{1 - \left(1 + \dfrac{r}{m}\right)^{-mt}}\right] \\[10ex] PMT = \dfrac{PV}{m} * \left[\dfrac{r}{1 - \left(1 + \dfrac{r}{m}\right)^{-1 * m * t}}\right] \\[10ex] PMT = \dfrac{10000}{12} * \left[\dfrac{0.07}{1 - \left(1 + \dfrac{0.07}{12}\right)^{-1 * 12 * 4}}\right] \\[10ex] = \dfrac{10000}{12} * \left[\dfrac{0.07}{1 - \left(1 + 0.00583333333\right)^{-48}}\right] \\[7ex] = \dfrac{10000}{12} * \left[\dfrac{0.07}{1 - \left(1.00583333333\right)^{-48}}\right] \\[7ex] = \dfrac{10000}{12} * \left[\dfrac{0.07}{1 - 0.756398825}\right] \\[5ex] = \dfrac{10000}{12} * \left[\dfrac{0.07}{0.243601175}\right] \\[5ex] = \dfrac{10000 * 0.07}{12 * 0.243601175} \\[5ex] = \dfrac{700}{2.9232141} \\[5ex] = 239.462446 \\[3ex] PMT \approx \$239.46 \\[3ex] (b.) \\[3ex] CI = PMT * m * t - PV \\[3ex] CI = 239.462446 * 12 * 4 - 10000 \\[3ex] = 11494.1974 - 10000 \\[3ex] = 1494.1974 \\[3ex] CI \approx \$1494.20 $

(2.) What monthly payment is required to amortize a loan of $30,000 over 13 years if interest at the rate of 3% per year is charged on the unpaid balance and interest calculations are made at the end of each month?

This is a case of Amortization

$ \underline{Amortization} \\[3ex] PV = \$30000 \\[3ex] r = 3\% = \dfrac{3}{100} = 0.03 \\[5ex] t = 13\: years \\[3ex] Compounded\:\:monthly \rightarrow m = 12 \\[3ex] PMT = ? \\[3ex] PMT = \dfrac{PV}{m} * \left[\dfrac{r}{1 - \left(1 + \dfrac{r}{m}\right)^{-mt}}\right] \\[10ex] PMT = \dfrac{PV}{m} * \left[\dfrac{r}{1 - \left(1 + \dfrac{r}{m}\right)^{-1 * m * t}}\right] \\[10ex] PMT = \dfrac{30000}{12} * \left[\dfrac{0.03}{1 - \left(1 + \dfrac{0.03}{12}\right)^{-1 * 12 * 13}}\right] \\[10ex] = 2500 * \left[\dfrac{0.03}{1 - \left(1 + 0.0025\right)^{-156}}\right] \\[7ex] = 2500 * \left[\dfrac{0.03}{1 - \left(1.0025\right)^{-156}}\right] \\[7ex] = 2500 * \left[\dfrac{0.03}{1 - 0.677386471}\right] \\[5ex] = 2500 * \left[\dfrac{0.03}{0.322613529}\right] \\[5ex] = \dfrac{2500 * 0.03}{0.322613529} \\[5ex] = \dfrac{75}{0.322613529} \\[5ex] = 232.476301 \\[3ex] PMT \approx \$232.48 \\[3ex] $

(3.) The price of a home in the City of Truth or Consequences, New Mexico is $139,000.
The bank requires a 20% down payment and 3 points at the time of closing.
Dove Bank has agreed to finance the home with a 30-year fixed-rate mortgage at 10%.
(a.) What is down payment?
(b.) Find the amount of the mortgage.
(c.) How much must be paid for 3 points of closing?
(d.) Calculate the monthly payment. Exclude taxes and insurance.
(e.) Calculate the total interest over the period of the loan.

This is a case of Amortization

$ (a.) \\[3ex] Down\:\:Payment = Given\:\:Rate * Purchase\:\:Price \\[3ex] Given\:\:Rate = 20\% = \dfrac{20}{100} = 0.2 \\[5ex] Purchase\:\:Price = \$139000 \\[3ex] Down\:\:Payment = 0.2(139000) = \$27,800.00 \\[3ex] (b.) \\[3ex] Amount\:\:of\:\:Mortgage = Purchase\:\:Price - Down\:\:Payment \\[3ex] Amount\:\:of\:\:Mortgage = 139000 - 27800 \\[3ex] Amount\:\:of\:\:Mortgage = \$111,200.00 \\[3ex] (c.) \\[3ex] Payment\:\:for\:\:x\:\:points\:\:at\:closing = x\:\:as\:\:\% * Amount\:\:of\:\:Mortgage \\[3ex] 3\:\:points\:\:at\:closing = 3\% = \dfrac{3}{100} = 0.03 \\[5ex] Payment\:\:for\:\:3\:\:points\:\:at\:closing = 3\% * 111200 = 0.03(111200) = \$3,336.00 \\[3ex] (d.) \\[3ex] PV = Amount\:\:of\:\:Mortgage = \$111200 \\[3ex] t = 30\: years \\[3ex] r = 10\% = \dfrac{10}{100} = 0.1 \\[5ex] Compounded\:\:monthly \rightarrow m = 12 \\[3ex] PMT = ? \\[3ex] PMT = \dfrac{PV}{m} * \left[\dfrac{r}{1 - \left(1 + \dfrac{r}{m}\right)^{-mt}}\right] \\[10ex] PMT = \dfrac{PV}{m} * \left[\dfrac{r}{1 - \left(1 + \dfrac{r}{m}\right)^{-1 * m * t}}\right] \\[10ex] PMT = \dfrac{111200}{12} * \left[\dfrac{0.1}{1 - \left(1 + \dfrac{0.1}{12}\right)^{-1 * 12 * 30}}\right] \\[10ex] = \dfrac{111200}{12} * \left[\dfrac{0.1}{1 - \left(1 + 0.00833333333\right)^{-360}}\right] \\[7ex] = \dfrac{111200}{12} * \left[\dfrac{0.1}{1 - \left(1.00833333333\right)^{-360}}\right] \\[7ex] = \dfrac{111200}{12} * \left[\dfrac{0.1}{1 - 0.0504098336}\right] \\[5ex] = \dfrac{111200}{12} * \left[\dfrac{0.1}{0.949590166}\right] \\[5ex] = \dfrac{111200 * 0.1}{12 * 0.949590166} \\[5ex] = \dfrac{11120}{11.395082} \\[5ex] = 975.859586 \\[3ex] PMT \approx \$975.86 \\[3ex] (e.) \\[3ex] CI = PMT * m * t - PV \\[3ex] CI = 975.859586 * 12 * 30 - 111200 \\[3ex] = 351309.451 - 111200 \\[3ex] = 240109.451 \\[3ex] CI \approx \$240,109.45 $

(4.) Paul is shopping for a new car.
He found a nice energy-efficient car he liked, and negotiated a good price with the dealer: $21,995 including taxes and license fees.
In addition, the car manufacturer offered him two options:

First Option: He can choose a $2000 manufacturer's rebate and then finance the balance at the dealer's going rate of 6% APR (Annual Percentage Rate) for a 60-month loan.

Second Option: He can use a special financing at 2.4% APR for 60 months.

(a.) Which option should he choose? Justify your answer.
(b.) How much savings would he have when comparing the two options over the period of the loan?

This is a case of Amortization

$ \underline{Amortization} \\[3ex] (a.) \\[3ex] \underline{Option\:1} \\[3ex] Rebate = \$2000 \\[3ex] PV = \$21995 - \$2000 = \$19995 \\[3ex] t = 60\:months =\dfrac{60}{12}\:years = 5\: years \\[5ex] r = 6\% = \dfrac{6}{100} = 0.06 \\[5ex] Compounded\:\:monthly \rightarrow m = 12 \\[3ex] PMT = ? \\[3ex] PMT = \dfrac{PV}{m} * \left[\dfrac{r}{1 - \left(1 + \dfrac{r}{m}\right)^{-mt}}\right] \\[10ex] PMT = \dfrac{PV}{m} * \left[\dfrac{r}{1 - \left(1 + \dfrac{r}{m}\right)^{-1 * m * t}}\right] \\[10ex] PMT = \dfrac{19995}{12} * \left[\dfrac{0.06}{1 - \left(1 + \dfrac{0.06}{12}\right)^{-1 * 12 * 5}}\right] \\[10ex] = \dfrac{19995}{12} * \left[\dfrac{0.06}{1 - \left(1 + 0.005\right)^{-60}}\right] \\[7ex] = \dfrac{19995}{12} * \left[\dfrac{0.06}{1 - \left(1.005\right)^{-60}}\right] \\[7ex] = \dfrac{19995}{12} * \left[\dfrac{0.06}{1 - 0.741372196}\right] \\[5ex] = \dfrac{19995}{12} * \left[\dfrac{0.06}{0.258627804}\right] \\[5ex] = \dfrac{19995 * 0.06}{12 * 0.258627804} \\[5ex] = \dfrac{1199.7}{3.10353365} \\[5ex] = 386.559366 \\[3ex] PMT \approx \$386.56 \\[3ex] \underline{Option\:2} \\[3ex] PV = \$21995 \\[3ex] t = 60\:months =\dfrac{60}{12}\:years = 5\: years \\[5ex] r = 2.4\% = \dfrac{2.4}{100} = 0.024 \\[5ex] Compounded\:\:monthly \rightarrow m = 12 \\[3ex] PMT = ? \\[3ex] PMT = \dfrac{PV}{m} * \left[\dfrac{r}{1 - \left(1 + \dfrac{r}{m}\right)^{-mt}}\right] \\[10ex] PMT = \dfrac{PV}{m} * \left[\dfrac{r}{1 - \left(1 + \dfrac{r}{m}\right)^{-1 * m * t}}\right] \\[10ex] PMT = \dfrac{21995}{12} * \left[\dfrac{0.024}{1 - \left(1 + \dfrac{0.024}{12}\right)^{-1 * 12 * 5}}\right] \\[10ex] = \dfrac{21995}{12} * \left[\dfrac{0.024}{1 - \left(1 + 0.002\right)^{-60}}\right] \\[7ex] = \dfrac{21995}{12} * \left[\dfrac{0.024}{1 - \left(1.002\right)^{-60}}\right] \\[7ex] = \dfrac{21995}{12} * \left[\dfrac{0.024}{1 - 0.887026732}\right] \\[5ex] = \dfrac{21995}{12} * \left[\dfrac{0.024}{0.112973268}\right] \\[5ex] = \dfrac{21995 * 0.024}{12 * 0.112973268} \\[5ex] = \dfrac{527.88}{1.35567922} \\[5ex] = 389.384149 \\[3ex] PMT \approx \$389.38 \\[3ex] \$386.56 \lt \$389.38 \\[3ex] He\:\:should\:\:choose\:\:Option\:1 \\[3ex] (b.) \\[3ex] Savings\:\:per\:\:month = 389.384149 - 386.559366 = \$2.824783 \\[3ex] Savings\:\:per\:\:month \approx \$2.82 \\[3ex] Savings\:\:over\:\:60\:months = 2.82(60) = \$169.20 $

(5.) A loan of $72,000.00 was taken for 30 years at 4.8% interest compounded quarterly.
Complete the table below. Fill only the boxes with the dollar symbol.
Round all answers to 2 decimal places.

Payment Number	Payment Amount	Principal Amount	Interest	Balance
$(0.)$				$\$72,000.00$
$(1.)$	$\$...$	$\$...$	$\$...$	$\$...$
$(2.)$		$\$...$	$\$...$	$\$...$
$(3.)$		$\$...$	$\$...$	$\$...$

This is a case of Amortization

$ PV = \$72000 \\[3ex] t = 30\: years \\[3ex] r = 4.8\% = \dfrac{4.8}{100} = 0.048 \\[5ex] Compounded\:\:quarterly \rightarrow m = 4 \\[3ex] PMT = ? \\[3ex] PMT = \dfrac{PV}{m} * \left[\dfrac{r}{1 - \left(1 + \dfrac{r}{m}\right)^{-mt}}\right] \\[10ex] PMT = \dfrac{PV}{m} * \left[\dfrac{r}{1 - \left(1 + \dfrac{r}{m}\right)^{-1 * m * t}}\right] \\[10ex] PMT = \dfrac{72000}{4} * \left[\dfrac{0.048}{1 - \left(1 + \dfrac{0.048}{4}\right)^{-1 * 4 * 30}}\right] \\[10ex] = 18000 * \left[\dfrac{0.048}{1 - \left(1 + 0.012\right)^{-120}}\right] \\[7ex] = 18000 * \left[\dfrac{0.048}{1 - \left(1.012\right)^{-120}}\right] \\[7ex] = 18000 * \left[\dfrac{0.048}{1 - 0.238967313}\right] \\[5ex] = 18000 * \left[\dfrac{0.048}{0.761032687}\right] \\[5ex] = \dfrac{18000 * 0.048}{0.761032687} \\[5ex] = \dfrac{864}{0.761032687} \\[5ex] = 1135.39946 \\[3ex] PMT \approx \color{darkblue}{\$1135.30}\\[3ex] $

Payment Number	Payment Amount	Principal Amount	Interest	Balance
$(0.)$				$\$72,000.00$
$(1.)$	$\color{darkblue}{\$1,135.30}$	$\color{purple}{\$271.30}$	$\color{black}{\$864.00}$	$71,728.70$
$(2.)$		$\color{purple}{\$274.56}$	$\color{black}{\$860.74}$	$71,454.14$
$(3.)$		$\color{purple}{\$277.85}$	$\color{black}{\$857.45}$	$\$71,176.29$

$ \underline{Payment\:\:Number\:1} \\[3ex] Interest = P * r * t = 72000 * 0.048 * \dfrac{1}{4} = \color{black}{\$864.00} \\[5ex] Principal\:\:Amount = Monthly\:\:Payment - Interest \\[3ex] Principal\:\:Amount = 1135.30 - 864.00 = \color{purple}{\$271.30} \\[3ex] Balance\:\:of\:\:Loan = Balance - Principal\:\:Amount \\[3ex] Balance\:\:of\:\:Loan = 72000.00 - 271.30 = \$71728.70 \\[3ex] $ NOTE: For the first payment:
The Principal Amount is the Amount of Mortgage
The Principal is also the Amount of Mortgage.

For the second payment:
The Principal Amount is the Principal for the second payment.
The Principal Amount is also the Balance of Loan after the first payment.

For the third payment:
The Principal Amount is the Principal for the third payment.
The Principal Amount is also the Balance of Loan after the second payment.

...and so on...and so forth...

$ \underline{Payment\:\:Number\:2} \\[3ex] Interest = P * r * t = 71728.70 * 0.048 * \dfrac{1}{4} = 860.7444 \approx \color{black}{\$860.74} \\[5ex] Principal\:\:Amount = Monthly\:\:Payment - Interest \\[3ex] Principal\:\:Amount = 1135.30 - 860.7444 = 274.5556 \approx \color{purple}{\$274.56} \\[3ex] Balance\:\:of\:\:Loan = Balance - Principal\:\:Amount \\[3ex] Balance\:\:of\:\:Loan = 71728.70 - 274.5556 = 71454.1444 \approx \$71454.14 \\[3ex] \underline{Payment\:\:Number\:3} \\[3ex] Interest = P * r * t = 71454.14 * 0.048 * \dfrac{1}{4} = 857.44968 \approx \color{black}{\$857.45} \\[5ex] Principal\:\:Amount = Monthly\:\:Payment - Interest \\[3ex] Principal\:\:Amount = 1135.30 - 857.44968 = 277.85032 \approx \color{purple}{\$277.85} \\[3ex] Balance\:\:of\:\:Loan = Balance - Principal\:\:Amount \\[3ex] Balance\:\:of\:\:Loan = 71454.14 - 277.85032 = 71176.2897 \approx \$71176.29 $

(6.) Grace Auto Sales is offering a financing package consisting of a 4.5% APR (Annual Percentage Rate) compounded monthly for a term of 4 years for their used vehicles.
Rebecca wants her monthly payments to be at most $400.
What is the maximum amount that she should finance?

This is a case of Present Value of Ordinary Annuity

$ r = 4.5\% = \dfrac{4.5}{100} = 0.045 \\[5ex] Compounded\:\:monthly \rightarrow m = 12 \\[3ex] t = 4\:years \\[3ex] PMT = \$400 \\[3ex] PV = m * PMT * \left[\dfrac{1 - \left(1 + \dfrac{r}{m}\right)^{-mt}}{r}\right] \\[10ex] PV = m * PMT * \left[\dfrac{1 - \left(1 + \dfrac{r}{m}\right)^{-1 * m * t}}{r}\right] \\[10ex] PV = 12 * 400 * \left[\dfrac{1 - \left(1 + \dfrac{0.045}{12}\right)^{-1 * 12 * 4}}{0.045}\right] \\[10ex] = 4800 * \left[\dfrac{1 - \left(1 + 0.00375\right)^{-48}}{0.045}\right] \\[7ex] = 4800 * \left[\dfrac{1 - \left(1.00375\right)^{-48}}{0.045}\right] \\[7ex] = 4800 * \left[\dfrac{1 - 0.83555146}{0.045}\right] \\[5ex] = 4800 * \left[\dfrac{0.16444854}{0.045}\right] \\[5ex] = \dfrac{4800 * 0.16444854}{0.045} \\[5ex] = \dfrac{789.352992}{0.045} \\[5ex] = 17541.1776 \\[3ex] PV \approx \$17,541.18 \\[3ex] $ The maximum amount that she should finance is $\$17,541.18$

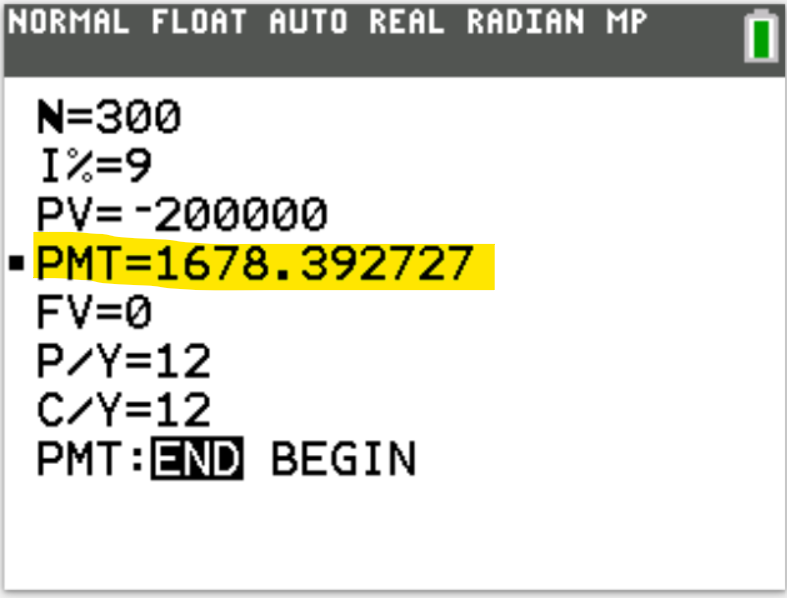
(7.) The Luke's family just closed on a 15-year mortgage home for $120,000 at 7% per annum.
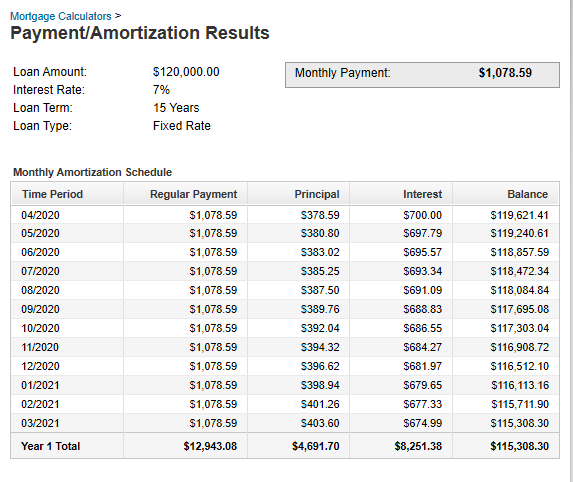
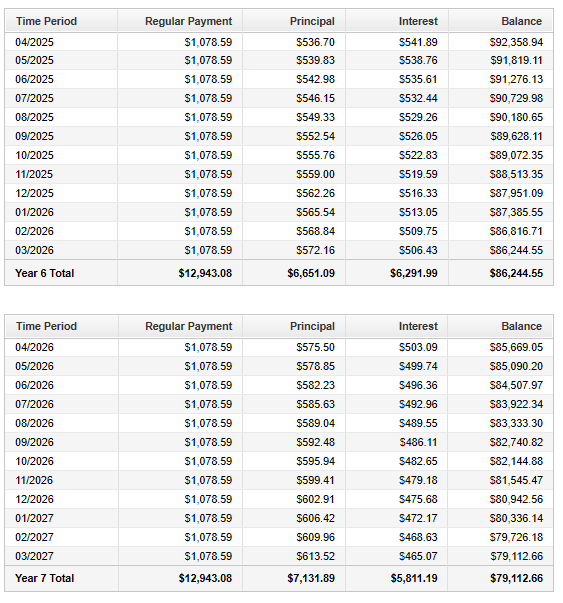
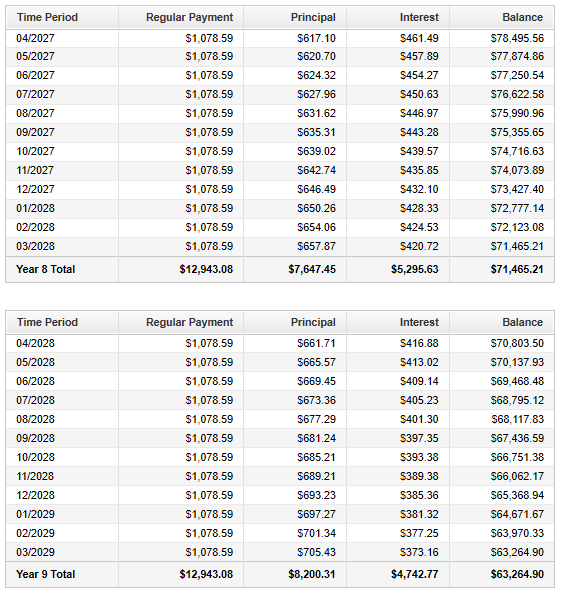
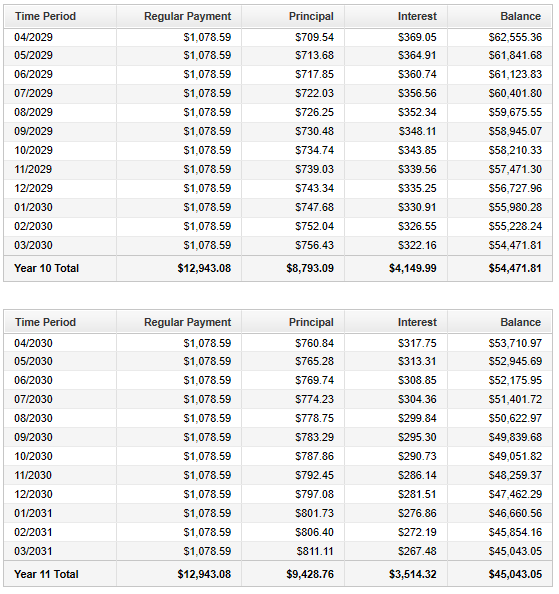
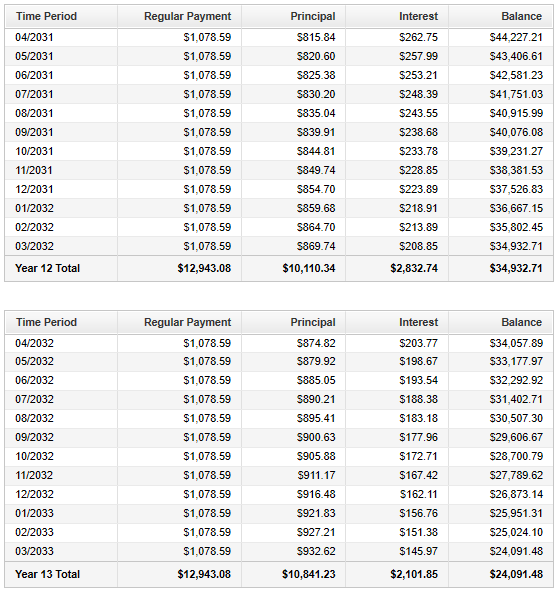
Angel Bank is financing the home.
Prepare a Loan Amortization Schedule for the mortgage.

This is a case of Amortization

$ PV = \$120000 \\[3ex] t = 15\: years \\[3ex] r = 7\% = \dfrac{7}{100} = 0.07 \\[5ex] Compounded\:\:monthly \rightarrow m = 12 \\[3ex] PMT = ? \\[3ex] PMT = \dfrac{PV}{m} * \left[\dfrac{r}{1 - \left(1 + \dfrac{r}{m}\right)^{-mt}}\right] \\[10ex] PMT = \dfrac{PV}{m} * \left[\dfrac{r}{1 - \left(1 + \dfrac{r}{m}\right)^{-1 * m * t}}\right] \\[10ex] PMT = \dfrac{120000}{12} * \left[\dfrac{0.07}{1 - \left(1 + \dfrac{0.07}{12}\right)^{-1 * 12 * 15}}\right] \\[10ex] = 10000 * \left[\dfrac{0.07}{1 - \left(1 + 0.00583333333\right)^{-180}}\right] \\[7ex] = 10000 * \left[\dfrac{0.07}{1 - \left(1.00583333333\right)^{-180}}\right] \\[7ex] = 10000 * \left[\dfrac{0.07}{1 - 0.351006914}\right] \\[5ex] = 10000 * \left[\dfrac{0.07}{0.648993086}\right] \\[5ex] = \dfrac{10000 * 0.07}{0.648993086} \\[5ex] = \dfrac{700}{0.648993086} \\[5ex] = 1078.59393 \\[3ex] PMT \approx \$1078.59\\[3ex] Number\:\:of\:\:payments = m * t \\[3ex] Number\:\:of\:\:payments = 12 * 15 = 180\:payments \\[3ex] $

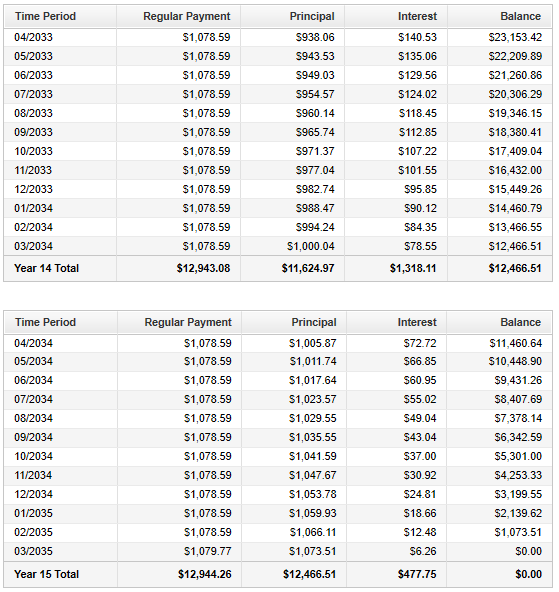
Loan Amortization Schedule for the Luke's Family
Annual $\%$Rate: $7\%$ Amount of Mortgage: $\$120,000$ Number of Monthly Payments: $180$		Monthly Payment: $\$1,078.59$ Term: Years $15$, Months $0$
Payment Number	Interest Payment	Principal Payment	Balance of Loan
$1$	$\$700.00$	$\$378.59$	$\$119,621.41$
$2$	$\$697.79$	$\$380.80$	$\$119,240.61$
Complete it	Complete it	Complete it	Complete it

$ \underline{Payment\:\:Number\:1} \\[3ex] Interest\:\:Payment = P * r * t = 120000 * 0.07 * \dfrac{1}{12} = \$700.00 \\[5ex] Principal\:\:Payment = Monthly\:\:Payment - Interest\:\:Payment \\[3ex] Principal\:\:Payment = 1078.59 - 700.00 = \$378.59 \\[3ex] Balance\:\:of\:\:Loan = Principal\:\:Balance - Principal\:\:Payment \\[3ex] Balance\:\:of\:\:Loan = 120000.00 - 378.59 = \$119621.41 \\[3ex] $ NOTE: For the first payment:
The Principal Balance is the Amount of Mortgage
The Principal is also the Amount of Mortgage.

For the second payment:
The Principal Balance is the Principal for the second payment.
The Principal Balance is also the Balance of Loan after the first payment.

For the third payment:
The Principal Balance is the Principal for the third payment.
The Principal Balance is also the Balance of Loan after the second payment.

...and so on...and so forth...

$ \underline{Payment\:\:Number\:2} \\[3ex] Interest\:\:Payment = P * r * t = 119621.41 * 0.07 * \dfrac{1}{12} = \$697.79 \\[5ex] Principal\:\:Payment = Monthly\:\:Payment - Interest\:\:Payment \\[3ex] Principal\:\:Payment = 1078.59 - 697.79 = \$380.80 \\[3ex] Balance\:\:of\:\:Loan = Principal\:\:Balance - Principal\:\:Payment \\[3ex] Balance\:\:of\:\:Loan = 119621.41 - 380.80 = \$119240.61 \\[3ex] $ Complete the rest of the Loan Amortization Table.
Check your answers with the calculator (please see the top page)
You can also check your answers using the table below.

Loan Amortization Table: Number 7: Part 1

Loan Amortization Table: Number 7: Part 2

Loan Amortization Table: Number 7: Part 3

Loan Amortization Table: Number 7: Part 4

Loan Amortization Table: Number 7: Part 5

Loan Amortization Table: Number 7: Part 6

Loan Amortization Table: Number 7: Part 7

Loan Amortization Table: Number 7: Part 8

Loan Amortization Table: Number 7: Part 9

(8.) Payments are made at the end of each month into an ordinary annuity earning interest at the rate of 2.25% per year compounded monthly for $9\dfrac{1}{4}$ years.
If the present value of the annuity is $45,000, determine the size of each payment.

This is a case of Amortization

$ PV = \$45000 \\[3ex] t = 9\dfrac{1}{4} = 9.25\: years \\[5ex] r = 2.25\% = \dfrac{2.25}{100} = 0.0225 \\[5ex] Compounded\:\:monthly \rightarrow m = 12 \\[3ex] PMT = ? \\[3ex] PMT = \dfrac{PV}{m} * \left[\dfrac{r}{1 - \left(1 + \dfrac{r}{m}\right)^{-mt}}\right] \\[10ex] PMT = \dfrac{PV}{m} * \left[\dfrac{r}{1 - \left(1 + \dfrac{r}{m}\right)^{-1 * m * t}}\right] \\[10ex] PMT = \dfrac{45000}{12} * \left[\dfrac{0.0225}{1 - \left(1 + \dfrac{0.0225}{12}\right)^{-1 * 12 * 9.25}}\right] \\[10ex] = 3750 * \left[\dfrac{0.0225}{1 - \left(1 + 0.001875\right)^{-111}}\right] \\[7ex] = 3750 * \left[\dfrac{0.0225}{1 - \left(1.001875\right)^{-111}}\right] \\[7ex] = 3750 * \left[\dfrac{0.0225}{1 - 0.8122637906}\right] \\[5ex] = 3750 * \left[\dfrac{0.0225}{0.1877362094}\right] \\[5ex] = \dfrac{3750 * 0.0225}{0.1877362094} \\[5ex] = \dfrac{84.375}{0.1877362094} \\[5ex] = 449.4338107 \\[3ex] PMT \approx \$449.43 $

(9.) The Peters wants to refinance their home.
The outstanding balance on their original loan is $120,000
They were offered two options by their bank.

First Option: Fixed-rate mortgage of 5.5% per year compounded monthly to be paid in 300 equal monthly installments over a 25-year period.

Second Option: Fixed-rate mortgage of 5.25% per year compounded monthly to be paid in 180 equal monthly installments over a 15-year period.

(a.) Calculate the monthly payments needed to amortize the loan amount for both options.
(b.) How much interest would the Peters save if they choose the 15-year mortgage rather than the 25-year mortgage?

This is a case of Amortization

$ (a.) \\[3ex] \underline{Option\:\:A} \\[3ex] PV = \$120000 \\[3ex] t = 25\: years \\[3ex] r = 5.5\% = \dfrac{5.5}{100} = 0.055 \\[5ex] Compounded\:\:monthly \rightarrow m = 12 \\[3ex] PMT = ? \\[3ex] PMT = \dfrac{PV}{m} * \left[\dfrac{r}{1 - \left(1 + \dfrac{r}{m}\right)^{-mt}}\right] \\[10ex] PMT = \dfrac{PV}{m} * \left[\dfrac{r}{1 - \left(1 + \dfrac{r}{m}\right)^{-1 * m * t}}\right] \\[10ex] PMT = \dfrac{120000}{12} * \left[\dfrac{0.055}{1 - \left(1 + \dfrac{0.055}{12}\right)^{-1 * 12 * 25}}\right] \\[10ex] = 10000 * \left[\dfrac{0.055}{1 - \left(1 + 0.004583333\right)^{-300}}\right] \\[7ex] = 10000 * \left[\dfrac{0.055}{1 - \left(1.004583333\right)^{-300}}\right] \\[7ex] = 10000 * \left[\dfrac{0.055}{1 - 0.2536351268}\right] \\[5ex] = 10000 * \left[\dfrac{0.055}{0.7463648732}\right] \\[5ex] = \dfrac{10000 * 0.055}{0.7463648732} \\[5ex] = \dfrac{550}{0.7463648732} \\[5ex] = 736.9049907 \\[3ex] PMT \approx \$736.90 \\[3ex] Total\:\:Payments = 736.9049907 * 12 * 25 = \$221071.4972 \\[3ex] Total\:\:Interest = Total\:\:Payments - Amount\:\:of\:\:Mortgage \\[3ex] Total\:\:Interest = 221071.4972 - 120000 = 101071.4972 \\[3ex] Total\:\:Interest \approx \$101,071.50 \\[5ex] \underline{Option\:\:B} \\[3ex] PV = \$120000 \\[3ex] t = 25\: years \\[3ex] r = 5.25\% = \dfrac{5.25}{100} = 0.0525 \\[5ex] Compounded\:\:monthly \rightarrow m = 12 \\[3ex] PMT = ? \\[3ex] PMT = \dfrac{PV}{m} * \left[\dfrac{r}{1 - \left(1 + \dfrac{r}{m}\right)^{-mt}}\right] \\[10ex] PMT = \dfrac{PV}{m} * \left[\dfrac{r}{1 - \left(1 + \dfrac{r}{m}\right)^{-1 * m * t}}\right] \\[10ex] PMT = \dfrac{120000}{12} * \left[\dfrac{0.0525}{1 - \left(1 + \dfrac{0.0525}{12}\right)^{-1 * 12 * 25}}\right] \\[10ex] = 10000 * \left[\dfrac{0.0525}{1 - \left(1 + 0.004375\right)^{-300}}\right] \\[7ex] = 10000 * \left[\dfrac{0.0525}{1 - \left(1.004375\right)^{-300}}\right] \\[7ex] = 10000 * \left[\dfrac{0.0525}{1 - 0.2699179506}\right] \\[5ex] = 10000 * \left[\dfrac{0.0525}{0.7300820494}\right] \\[5ex] = \dfrac{10000 * 0.0525}{0.7300820494} \\[5ex] = \dfrac{525}{0.7300820494} \\[5ex] = 719.0972582 \\[3ex] PMT \approx \$719.10 \\[3ex] Total\:\:Payments = 719.0972582 * 12 * 25 = \$215729.1775 \\[3ex] Total\:\:Interest = Total\:\:Payments - Amount\:\:of\:\:Mortgage \\[3ex] Total\:\:Interest = 215729.1775 - 120000 = 95729.17747 \\[3ex] Total\:\:Interest \approx \$95,729.18 \\[5ex] (b.) \\[3ex] Interest\:\:Savings\:\:by\:\:choosing\:\:15-year\:\:mortgage \\[3ex] = 101071.4972 - 95729.17747 \\[3ex] = 5342.319734 \\[3ex] \approx \$5,342.32 $

(10.) The price of a new Jaguar Jeep is $24,000
Augustine makes a down payment of 25% towards the purchase of the car.
He secures financing for the balance at the rate of 9% per year compounded monthly.
(a.) What monthly payment will he be required to make if the car is financed overa period of 36 months?
(b.) Calculate the interest charges for the 36-month financing plan.

This is a case of Amortization

$ Purchase\:\:Price = \$24000 \\[3ex] 25\%\:\:down\:\:payment = \dfrac{25}{100} * 24000 = 25(24) = \$6000 \\[5ex] (a.) \\[3ex] PV = \$24000 - \$6000 = \$18000 \\[3ex] t = 36\: months = 3\:years \\[3ex] r = 9\% = \dfrac{9}{100} = 0.09 \\[5ex] Compounded\:\:monthly \rightarrow m = 12 \\[3ex] PMT = ? \\[3ex] PMT = \dfrac{PV}{m} * \left[\dfrac{r}{1 - \left(1 + \dfrac{r}{m}\right)^{-mt}}\right] \\[10ex] PMT = \dfrac{PV}{m} * \left[\dfrac{r}{1 - \left(1 + \dfrac{r}{m}\right)^{-1 * m * t}}\right] \\[10ex] PMT = \dfrac{18000}{12} * \left[\dfrac{0.09}{1 - \left(1 + \dfrac{0.09}{12}\right)^{-1 * 12 * 3}}\right] \\[10ex] = 1500 * \left[\dfrac{0.09}{1 - \left(1 + 0.0075\right)^{-36}}\right] \\[7ex] = 1500 * \left[\dfrac{0.09}{1 - \left(1.0075\right)^{-36}}\right] \\[7ex] = 1500 * \left[\dfrac{0.09}{1 - 0.7641489606}\right] \\[5ex] = 1500 * \left[\dfrac{0.09}{0.2358510394}\right] \\[5ex] = \dfrac{1500 * 0.09}{0.2358510394} \\[5ex] = \dfrac{135}{0.2358510394} \\[5ex] = 572.3951878 \\[3ex] PMT \approx \$572.40 \\[3ex] (b.) \\[3ex] Interest = PMT * m * t - PV \\[3ex] Interest = 572.3951878 * 12 * 3 - 18000 \\[3ex] = 20606.22676 - 18000 \\[3ex] = 2606.226762 \\[3ex] Interest \approx \$2606.23 $

(11.) To start an automobile sales firm, Paul borrwed a $10,000 loan from his bank 4 years ago.
His bank charged a 3% interest rate per year compounded monthly on the loan.
Paul wants to repay the loan at the same interest rate by amortizing it through monthly payments over 10 years.
Calculate his monthly payments.

This is a case of Compound Interest and Amortization

$ (a.) \\[3ex] Compound\:\:Interest \\[3ex] P = \$10000 \\[3ex] t = 4\: years \\[3ex] r = 3\% = \dfrac{3}{100} = 0.03 \\[5ex] Compounded\:\:monthly \rightarrow m = 12 \\[3ex] A = ? \\[3ex] A = P\left(1 + \dfrac{r}{m}\right)^{mt} \\[5ex] A = 10000 * \left(1 + \dfrac{0.03}{12}\right)^{12 * 4} \\[5ex] = 10000 * \left(1 + 0.0025\right)^{48} \\[5ex] = 10000 * \left(1.0025\right)^{48} \\[5ex] = 10000 * 1.127328021 \\[3ex] A = 1127.328021 \\[3ex] Amortization \\[3ex] PV = A = \$11273.28021 \\[3ex] t = 10\: years \\[3ex] r = 3\% = \dfrac{3}{100} = 0.03 \\[5ex] Compounded\:\:monthly \rightarrow m = 12 \\[3ex] PMT = ? \\[3ex] PMT = \dfrac{PV}{m} * \left[\dfrac{r}{1 - \left(1 + \dfrac{r}{m}\right)^{-mt}}\right] \\[10ex] PMT = \dfrac{PV}{m} * \left[\dfrac{r}{1 - \left(1 + \dfrac{r}{m}\right)^{-1 * m * t}}\right] \\[10ex] PMT = \dfrac{11273.28021}{12} * \left[\dfrac{0.03}{1 - \left(1 + \dfrac{0.03}{12}\right)^{-1 * 12 * 10}}\right] \\[10ex] = 939.4400175 * \left[\dfrac{0.03}{1 - \left(1 + 0.0025\right)^{-120}}\right] \\[7ex] = 939.4400175 * \left[\dfrac{0.03}{1 - \left(1.0025\right)^{-120}}\right] \\[7ex] = 939.4400175 * \left[\dfrac{0.03}{1 - 0.7410956173}\right] \\[5ex] = 939.4400175 * \left[\dfrac{0.03}{0.2589043827}\right] \\[5ex] = \dfrac{939.4400175 * 0.03}{0.2589043827} \\[5ex] = \dfrac{28.18320053}{0.2589043827} \\[5ex] = 108.8556332 \\[3ex] PMT \approx \$108.86 $

(12.) Upright Capital, an investment firm purchased some acres of land for 5 million.
The firm made an initial down payment of 10% and obtained financing for the balance.
If the loan is to be amortized over 14 years at an interest rate of 5.1% per year compounded quarterly, find the required quarterly payment.

This is a case of Amortization

$ Purchase\:\:Price = \$5,000,000 \\[3ex] 10\%\:\:down\:\:payment = \dfrac{10}{100} * 5000000 = 25(24) = \$500000 \\[5ex] PV = \$5000000 - \$500000 = \$4500000 \\[3ex] t = 14\:years \\[3ex] r = 5.1\% = \dfrac{5.1}{100} = 0.051 \\[5ex] Compounded\:\:monthly \rightarrow m = 4 \\[3ex] PMT = ? \\[3ex] PMT = \dfrac{PV}{m} * \left[\dfrac{r}{1 - \left(1 + \dfrac{r}{m}\right)^{-mt}}\right] \\[10ex] PMT = \dfrac{PV}{m} * \left[\dfrac{r}{1 - \left(1 + \dfrac{r}{m}\right)^{-1 * m * t}}\right] \\[10ex] PMT = \dfrac{4500000}{4} * \left[\dfrac{0.051}{1 - \left(1 + \dfrac{0.051}{4}\right)^{-1 * 4 * 14}}\right] \\[10ex] = 1125000 * \left[\dfrac{0.051}{1 - \left(1 + 0.012575\right)^{-56}}\right] \\[7ex] = 1125000 * \left[\dfrac{0.051}{1 - \left(1.01275\right)^{-56}}\right] \\[7ex] = 1125000 * \left[\dfrac{0.051}{1 - 0.4918966854}\right] \\[5ex] = 1125000 * \left[\dfrac{0.051}{0.5081033146}\right] \\[5ex] = \dfrac{1125000 * 0.051}{0.5081033146} \\[5ex] = \dfrac{57375}{0.5081033146} \\[5ex] = 112919.9483 \\[3ex] PMT \approx \$112,919.95 $

(13.) Calculate the present value of a $300 per month ordinary annuity at 4% per year compounded monthly for 12 years.

This is a case of the Present Value of Ordinary Annuity

$ \underline{Present\:\:Value\:\:of\:\:Ordinary\:\:Annuity} \\[3ex] PMT = \$300 \\[3ex] r = 4\% = \dfrac{4}{100} = 0.04 \\[5ex] Compounded\:\:monthly \rightarrow m = 12 \\[3ex] t = 12\:years \\[3ex] PV = ? \\[3ex] PV = m * PMT * \left[\dfrac{1 - \left(1 + \dfrac{r}{m}\right)^{-mt}}{r}\right] \\[10ex] PV = m * PMT * \left[\dfrac{1 - \left(1 + \dfrac{r}{m}\right)^{-1 * m * t}}{r}\right] \\[10ex] PV = 12 * 300 * \left[\dfrac{1 - \left(1 + \dfrac{0.04}{12}\right)^{-1 * 12 * 12}}{0.04}\right] \\[10ex] = 3600 * \left[\dfrac{1 - \left(1 + 0.00333333333\right)^{-144}}{0.04}\right] \\[7ex] = 3600 * \left[\dfrac{1 - \left(1.00333333333\right)^{-144}}{0.04}\right] \\[7ex] = 3600 * \left[\dfrac{1 - 0.619277519}{0.04}\right] \\[5ex] = 3600 * \left[\dfrac{0.380722481}{0.04}\right] \\[5ex] = \dfrac{3600 * 0.380722481}{0.04} \\[5ex] = \dfrac{1370.60093}{0.04} \\[5ex] PV = 34265.0233 \\[3ex] PV \approx \$34,265.02 $

(14.) Felicity's parents set up a $27,000 trust fund for her.
She is to receive the money over a 6-year period in equal installments at the end of each year.
If the trust fund earns interest at the rate of 4% per year compounded annually, calculate the amount she will receive at the end of each year.

This is a case of Amortization

$ PV = \$27000 \\[3ex] t = 6\:years \\[3ex] r = 4\% = \dfrac{4}{100} = 0.04 \\[5ex] Compounded\:\:annually \rightarrow m = 1 \\[3ex] PMT = ? \\[3ex] PMT = \dfrac{PV}{m} * \left[\dfrac{r}{1 - \left(1 + \dfrac{r}{m}\right)^{-mt}}\right] \\[10ex] PMT = \dfrac{PV}{m} * \left[\dfrac{r}{1 - \left(1 + \dfrac{r}{m}\right)^{-1 * m * t}}\right] \\[10ex] PMT = \dfrac{27000}{1} * \left[\dfrac{0.04}{1 - \left(1 + \dfrac{0.04}{1}\right)^{-1 * 1 * 6}}\right] \\[10ex] = 27000 * \left[\dfrac{0.04}{1 - \left(1 + 0.04\right)^{-6}}\right] \\[7ex] = 27000 * \left[\dfrac{0.04}{1 - \left(1.04\right)^{-6}}\right] \\[7ex] = 27000 * \left[\dfrac{0.04}{1 - 0.7903145257}\right] \\[5ex] = 27000 * \left[\dfrac{0.04}{0.2096854743}\right] \\[5ex] = \dfrac{27000 * 0.04}{0.2096854743} \\[5ex] = \dfrac{1080}{0.2096854743} \\[5ex] = 5150.571367 \\[3ex] PMT \approx \$5,150.57 $

(15.) The Phoenician Hotels has agreed to pay Sarah $40$ installments of $25,000 per year in her lawsuit against them.
They intend to pay her $25,000 immediatley and will make the other payments at the end of each of each year for the remaining years.
How much should they have in the bank to guarantee the payments, assuming that the balance on deposit with the bank earns interest at the rate of 4% per year compounded yearly?

$40$ installmental payments
Immediate payment of $\$25000$
Remaining payments = $40 - 1 = 39$ payments = $39$ years
This is a case of the Present Value of Ordinary Annuity

$ \underline{Present\:\:Value\:\:of\:\:Ordinary\:\:Annuity} \\[3ex] PMT = \$25000 \\[3ex] r = 4\% = \dfrac{4}{100} = 0.04 \\[5ex] Compounded\:\:yearly \rightarrow m = 1 \\[3ex] t = 39\:years \\[3ex] PV = ? \\[3ex] PV = m * PMT * \left[\dfrac{1 - \left(1 + \dfrac{r}{m}\right)^{-mt}}{r}\right] \\[10ex] PV = m * PMT * \left[\dfrac{1 - \left(1 + \dfrac{r}{m}\right)^{-1 * m * t}}{r}\right] \\[10ex] PV = 1 * 25000 * \left[\dfrac{1 - \left(1 + \dfrac{0.04}{1}\right)^{-1 * 1 * 39}}{0.04}\right] \\[10ex] = 25000 * \left[\dfrac{1 - \left(1 + 0.04\right)^{-39}}{0.04}\right] \\[7ex] = 25000 * \left[\dfrac{1 - \left(1.04\right)^{-39}}{0.04}\right] \\[7ex] = 25000 * \left[\dfrac{1 - 0.2166206064}{0.04}\right] \\[5ex] = 25000 * \left[\dfrac{0.7833793936}{0.04}\right] \\[5ex] = \dfrac{25000 * 0.7833793936}{0.04} \\[5ex] = \dfrac{19584.48484}{0.04} \\[5ex] PV = 489612.121 \\[3ex] PV \approx \$489,612.12 \\[3ex] $ To guarantee payments, The Phoenician Hotels should have:

$ 25000 + 489612.121 \\[3ex] = 514612.121 \\[3ex] \approx \$514,612.12 $

(16.) The Marys' Family wants to buy a house.
They have a sum of $40,000 that they intend to use as a down payment.
To take advantage of tax deductions, they have decided to invest a minimum of $2800 and a maximum of $3400 per month toward the purchase of their house.
Assume the local mortgage rates are 4.5% per year compounded monthly for a conventional 30-year mortgage, calculate the price range of the houses (least expensive and most expensive) that should be in their budget.

This is a case of the Present Value of Ordinary Annuity

$ \underline{1st\;\;Case:\;\;Least\;\;Expensive} \\[3ex] PMT = \$2800 \\[3ex] r = 4.5\% = \dfrac{4.5}{100} = 0.045 \\[5ex] Compounded\:\:monthly \rightarrow m = 12 \\[3ex] t = 30\:years \\[3ex] PV = ? \\[3ex] PV = m * PMT * \left[\dfrac{1 - \left(1 + \dfrac{r}{m}\right)^{-mt}}{r}\right] \\[10ex] PV = m * PMT * \left[\dfrac{1 - \left(1 + \dfrac{r}{m}\right)^{-1 * m * t}}{r}\right] \\[10ex] PV = 12 * 2800 * \left[\dfrac{1 - \left(1 + \dfrac{0.045}{12}\right)^{-1 * 12 * 30}}{0.045}\right] \\[10ex] = 33600 * \left[\dfrac{1 - \left(1 + 0.00375\right)^{-360}}{0.045}\right] \\[7ex] = 33600 * \left[\dfrac{1 - \left(1.00375\right)^{-360}}{0.045}\right] \\[7ex] = 33600 * \left[\dfrac{1 - 0.2598956537}{0.045}\right] \\[5ex] = 33600 * \left[\dfrac{0.7401043463}{0.045}\right] \\[5ex] = \dfrac{33600 * 0.7401043463}{0.045} \\[5ex] = \dfrac{24867.50604}{0.045} \\[5ex] PV = 552611.2452 \\[3ex] $ In addition to the $40,000 down payment, the least expensive house in their budget is:

$ 40000 + 552611.2452 \\[3ex] = 592611.2452 \\[3ex] \approx \$592,611.25 \\[5ex] \underline{2nd\;\;Case:\;\;Most\;\;Expensive} \\[3ex] PMT = \$3400 \\[3ex] r = 4.5\% = \dfrac{4.5}{100} = 0.045 \\[5ex] Compounded\:\:monthly \rightarrow m = 12 \\[3ex] t = 30\:years \\[3ex] PV = ? \\[3ex] PV = m * PMT * \left[\dfrac{1 - \left(1 + \dfrac{r}{m}\right)^{-mt}}{r}\right] \\[10ex] PV = m * PMT * \left[\dfrac{1 - \left(1 + \dfrac{r}{m}\right)^{-1 * m * t}}{r}\right] \\[10ex] PV = 12 * 3400 * \left[\dfrac{1 - \left(1 + \dfrac{0.045}{12}\right)^{-1 * 12 * 30}}{0.045}\right] \\[10ex] = 40800 * \left[\dfrac{1 - \left(1 + 0.00375\right)^{-360}}{0.045}\right] \\[7ex] = 40800 * \left[\dfrac{1 - \left(1.00375\right)^{-360}}{0.045}\right] \\[7ex] = 40800 * \left[\dfrac{1 - 0.2598956537}{0.045}\right] \\[5ex] = 40800 * \left[\dfrac{0.7401043463}{0.045}\right] \\[5ex] = \dfrac{40800 * 0.7401043463}{0.045} \\[5ex] = \dfrac{30196.25733}{0.045} \\[5ex] PV = 671027.9406 \\[3ex] $ In addition to the $40,000 down payment, the most expensive house in their budget is:

$ 40000 + 671027.9406 \\[3ex] = 711027.9406 \\[3ex] \approx \$711,027.94 \\[3ex] $ ∴ the price range of the houses for their budget is: $592,611.25 to $711,027.94

(17.) Agnes took a 30-year adjustable-rate mortgage (ARM) of $250,000 with a 5% interest per year compounded monthly five years ago.
Presently, her interest rate is 5.5% per year compounded monthly.
What will be her new monthly payment?

This is a case of Amortization; the Present Value of Ordinary Annuity; and another Amortization

$ \underline{Amortization} \\[3ex] PV = \$250000 \\[3ex] t = 30\:years \\[3ex] r = 5\% = \dfrac{5}{100} = 0.05 \\[5ex] Compounded\:\:monthly \rightarrow m = 12 \\[3ex] PMT = ? \\[3ex] PMT = \dfrac{PV}{m} * \left[\dfrac{r}{1 - \left(1 + \dfrac{r}{m}\right)^{-mt}}\right] \\[10ex] PMT = \dfrac{PV}{m} * \left[\dfrac{r}{1 - \left(1 + \dfrac{r}{m}\right)^{-1 * m * t}}\right] \\[10ex] PMT = \dfrac{250000}{12} * \left[\dfrac{0.05}{1 - \left(1 + \dfrac{0.05}{12}\right)^{-1 * 12 * 30}}\right] \\[10ex] = 20833.33333 * \left[\dfrac{0.05}{1 - \left(1 + 0.004166666667\right)^{-360}}\right] \\[7ex] = 20833.33333 * \left[\dfrac{0.05}{1 - \left(1.004166667\right)^{-360}}\right] \\[7ex] = 20833.33333 * \left[\dfrac{0.05}{1 - 0.2238265956}\right] \\[5ex] = 20833.33333 * \left[\dfrac{0.05}{0.7761734044}\right] \\[5ex] = \dfrac{20833.33333 * 0.05}{0.7761734044} \\[5ex] = \dfrac{1041.666667}{0.7761734044} \\[5ex] = 1342.054057 \\[3ex] PMT \approx \$1,342.05 \\[3ex] $ This was $5$ years ago.
She made this monthly payments for $5$ years.
She still has $25$ years remaining.
To find the amount still owed in the house:

$ \underline{Present\:\:Value\:\:of\:\:Ordinary\:\:Annuity} \\[3ex] PMT = \$1342.054057 \\[3ex] r = 5\% = \dfrac{5}{100} = 0.05 \\[5ex] Compounded\:\:monthly \rightarrow m = 12 \\[3ex] t = 30 - 5 = 25\:years \\[3ex] PV = ? \\[3ex] PV = m * PMT * \left[\dfrac{1 - \left(1 + \dfrac{r}{m}\right)^{-mt}}{r}\right] \\[10ex] PV = m * PMT * \left[\dfrac{1 - \left(1 + \dfrac{r}{m}\right)^{-1 * m * t}}{r}\right] \\[10ex] PV = 12 * 1342.054057 * \left[\dfrac{1 - \left(1 + \dfrac{0.05}{12}\right)^{-1 * 12 * 25}}{0.05}\right] \\[10ex] = 16104.64869 * \left[\dfrac{1 - \left(1 + 0.004166666667\right)^{-300}}{0.05}\right] \\[7ex] = 16104.64869 * \left[\dfrac{1 - \left(1.004166667\right)^{-300}}{0.05}\right] \\[7ex] = 16104.64869 * \left[\dfrac{1 - 0.287249804}{0.05}\right] \\[5ex] = 16104.64869 * \left[\dfrac{0.712750196}{0.05}\right] \\[5ex] = \dfrac{16104.64869 * 0.712750196}{0.05} \\[5ex] = \dfrac{11478.59151}{0.05} \\[5ex] PV = 229571.8302 \\[3ex] PV \approx \$229,571.83 \\[3ex] $ Because her mortgage is an ARM, it has a variable interest rate.
Her new interest rate is $5.5\%$
To find her new monthly payment:

$ \underline{Amortization} \\[3ex] PV = \$229571.8302 \\[3ex] t = 25\:years \\[3ex] r = 5.5\% = \dfrac{5.5}{100} = 0.055 \\[5ex] Compounded\:\:monthly \rightarrow m = 12 \\[3ex] PMT = ? \\[3ex] PMT = \dfrac{PV}{m} * \left[\dfrac{r}{1 - \left(1 + \dfrac{r}{m}\right)^{-mt}}\right] \\[10ex] PMT = \dfrac{PV}{m} * \left[\dfrac{r}{1 - \left(1 + \dfrac{r}{m}\right)^{-1 * m * t}}\right] \\[10ex] PMT = \dfrac{229571.8302}{12} * \left[\dfrac{0.055}{1 - \left(1 + \dfrac{0.055}{12}\right)^{-1 * 12 * 25}}\right] \\[10ex] = 19130.98585 * \left[\dfrac{0.055}{1 - \left(1 + 0.004583333333\right)^{-300}}\right] \\[7ex] = 19130.98585 * \left[\dfrac{0.055}{1 - \left(1.004583333\right)^{-300}}\right] \\[7ex] = 19130.98585 * \left[\dfrac{0.055}{1 - 0.2536351268}\right] \\[5ex] = 19130.98585 * \left[\dfrac{0.055}{0.7463648732}\right] \\[5ex] = \dfrac{19130.98585 * 0.055}{0.7463648732} \\[5ex] = \dfrac{1052.204222}{0.7463648732} \\[5ex] = 1409.771895 \\[3ex] PMT \approx \$1,409.77 \\[3ex] $ The new monthly payments are $\$1,409.77$

(18.) Sixtus took a 15-year mortgage loan of $185,000 with a 3% per year interest rate compounded monthly on the unpaid balance.
He intends to sell the his house in ten years.
How much will he still owe on his house?

This is a case of Amortization and the Present Value of Ordinary Annuity

$ \underline{Amortization} \\[3ex] PV = \$185000 \\[3ex] t = 15\:years \\[3ex] r = 3\% = \dfrac{3}{100} = 0.03 \\[5ex] Compounded\:\:monthly \rightarrow m = 12 \\[3ex] PMT = ? \\[3ex] PMT = \dfrac{PV}{m} * \left[\dfrac{r}{1 - \left(1 + \dfrac{r}{m}\right)^{-mt}}\right] \\[10ex] PMT = \dfrac{PV}{m} * \left[\dfrac{r}{1 - \left(1 + \dfrac{r}{m}\right)^{-1 * m * t}}\right] \\[10ex] PMT = \dfrac{185000}{12} * \left[\dfrac{0.03}{1 - \left(1 + \dfrac{0.03}{12}\right)^{-1 * 12 * 15}}\right] \\[10ex] = 15416.66667 * \left[\dfrac{0.03}{1 - \left(1 + 0.0025\right)^{-180}}\right] \\[7ex] = 15416.66667 * \left[\dfrac{0.03}{1 - \left(1.0025\right)^{-180}}\right] \\[7ex] = 15416.66667 * \left[\dfrac{0.03}{1 - 0.6379863214}\right] \\[5ex] = 15416.66667 * \left[\dfrac{0.03}{0.3620136786}\right] \\[5ex] = \dfrac{15416.66667 * 0.03}{0.3620136786} \\[5ex] = \dfrac{462.5000001}{0.3620136786} \\[5ex] = 1277.576035 \\[3ex] PMT \approx \$1,277.58 \\[3ex] $ He plans to sell the house in $10$ years.
However, he has made his monthly payments for those payments.
So, he has $5$ years remaining.
To find the amount still owed in the house:

$ \underline{Present\:\:Value\:\:of\:\:Ordinary\:\:Annuity} \\[3ex] PMT = \$1277.576035 \\[3ex] r = 3\% = \dfrac{3}{100} = 0.03 \\[5ex] Compounded\:\:monthly \rightarrow m = 12 \\[3ex] t = 15 - 10 = 5\:years \\[3ex] PV = ? \\[3ex] PV = m * PMT * \left[\dfrac{1 - \left(1 + \dfrac{r}{m}\right)^{-mt}}{r}\right] \\[10ex] PV = m * PMT * \left[\dfrac{1 - \left(1 + \dfrac{r}{m}\right)^{-1 * m * t}}{r}\right] \\[10ex] PV = 12 * 1277.576035 * \left[\dfrac{1 - \left(1 + \dfrac{0.03}{12}\right)^{-1 * 12 * 5}}{0.03}\right] \\[10ex] = 15330.91242 * \left[\dfrac{1 - \left(1 + 0.0025\right)^{-60}}{0.03}\right] \\[7ex] = 15330.91242 * \left[\dfrac{1 - \left(1.0025\right)^{-60}}{0.03}\right] \\[7ex] = 15330.91242 * \left[\dfrac{1 - 0.8608691058}{0.03}\right] \\[5ex] = 15330.91242 * \left[\dfrac{0.1391308942}{0.03}\right] \\[5ex] = \dfrac{15330.91242 * 0.1391308942}{0.03} \\[5ex] = \dfrac{2133.003554}{0.03} \\[5ex] PV = 71100.11847 \\[3ex] PV \approx \$71,100.12 \\[3ex] $ He will still owe $\$71,100.12$ on his house.

(19.) Hannah purchased a $300,000 home.
She made an initial down payment of $40,000 and secured a mortgage with interest charged at the rate of 8% per year on the unpaid balance.
Interest computations are made at the end of each month.
If the loan is to be amortized over 30 years:
(a.) What monthly payment will Hannah be required to pay?
(b.) What is her equity (disregarding appreciation) after 5 years?

This is a case of Amortization and the Present Value of Ordinary Annuity

$ (a.) \\[3ex] \underline{Amortization} \\[3ex] Purchase\:\:price = \$300000 \\[3ex] Down\:\:payment = \$40000 \\[3ex] PV = 300000 - 40000 = \$260000 \\[3ex] t = 30\:years \\[3ex] r = 8\% = \dfrac{8}{100} = 0.08 \\[5ex] Compounded\:\:monthly \rightarrow m = 12 \\[3ex] PMT = ? \\[3ex] PMT = \dfrac{PV}{m} * \left[\dfrac{r}{1 - \left(1 + \dfrac{r}{m}\right)^{-mt}}\right] \\[10ex] PMT = \dfrac{PV}{m} * \left[\dfrac{r}{1 - \left(1 + \dfrac{r}{m}\right)^{-1 * m * t}}\right] \\[10ex] PMT = \dfrac{260000}{12} * \left[\dfrac{0.08}{1 - \left(1 + \dfrac{0.08}{12}\right)^{-1 * 12 * 30}}\right] \\[10ex] = 21666.66667 * \left[\dfrac{0.08}{1 - \left(1 + 0.006666666667\right)^{-360}}\right] \\[7ex] = 21666.66667 * \left[\dfrac{0.08}{1 - \left(1.006666667\right)^{-360}}\right] \\[7ex] = 21666.66667 * \left[\dfrac{0.08}{1 - 0.09144336154}\right] \\[5ex] = 21666.66667 * \left[\dfrac{0.08}{0.9085566385}\right] \\[5ex] = \dfrac{21666.66667 * 0.08}{0.9085566385} \\[5ex] = \dfrac{1733.333334}{0.9085566385} \\[5ex] = 1907.787869 \\[3ex] PMT \approx \$1,907.79 \\[3ex] $ To find the equity after $5$ years; we need to calculate the present value of her remaining payments.

$ (b.) \\[3ex] \underline{Present\:\:Value\:\:of\:\:Ordinary\:\:Annuity} \\[3ex] PMT = \$1907.787869 \\[3ex] r = 8\% = \dfrac{8}{100} = 0.08 \\[5ex] Compounded\:\:monthly \rightarrow m = 12 \\[3ex] t = 30 - 5 = 25\:years \\[3ex] PV = ? \\[3ex] PV = m * PMT * \left[\dfrac{1 - \left(1 + \dfrac{r}{m}\right)^{-mt}}{r}\right] \\[10ex] PV = m * PMT * \left[\dfrac{1 - \left(1 + \dfrac{r}{m}\right)^{-1 * m * t}}{r}\right] \\[10ex] PV = 12 * 1907.787869 * \left[\dfrac{1 - \left(1 + \dfrac{0.08}{12}\right)^{-1 * 12 * 25}}{0.08}\right] \\[10ex] = 22893.45443 * \left[\dfrac{1 - \left(1 + 0.006666666667\right)^{-300}}{0.08}\right] \\[7ex] = 22893.45443 * \left[\dfrac{1 - \left(1.006666667\right)^{-300}}{0.08}\right] \\[7ex] = 22893.45443 * \left[\dfrac{1 - 0.1362365024}{0.08}\right] \\[5ex] = 22893.45443 * \left[\dfrac{0.8637634976}{0.08}\right] \\[5ex] = \dfrac{22893.45443 * 0.8637634976}{0.08} \\[5ex] = \dfrac{19774.53027}{0.08} \\[5ex] PV = 247181.6284 \\[3ex] Equity = Purchase\:\:price + PV \\[3ex] Equity = 300000 + 247181.6284 \\[3ex] Equity = 547181.6284 \\[3ex] Equity \approx \$547,181.63 $

Top

(21.) For a home mortgage of $200,000 at a fixed APR of 9% for 25 years:
(a.) Calculate the monthly payment.
(b.) Determine the total amount paid over the term of the loan.
(c.) Of the total amount paid, what percentage is paid toward the principal and what percentage is paid for interest?

(a.) This is a case of Amortization
We can do this question using at least two approaches.
Use any approach you prefer.
1st Approach: By Formula

Answer: Number21first

$ PV = \$200000 \\[3ex] t = 25\:years \\[3ex] r = 9\% = \dfrac{9}{100} = 0.09 \\[5ex] Compounded\:\:monthly \rightarrow m = 12 \\[3ex] PMT = ? \\[3ex] PMT = \dfrac{PV}{m} * \left[\dfrac{r}{1 - \left(1 + \dfrac{r}{m}\right)^{-mt}}\right] \\[10ex] PMT = \dfrac{PV}{m} * \left[\dfrac{r}{1 - \left(1 + \dfrac{r}{m}\right)^{-1 * m * t}}\right] \\[10ex] PMT = \dfrac{200000}{12} * \left[\dfrac{0.09}{1 - \left(1 + \dfrac{0.09}{12}\right)^{-1 * 12 * 25}}\right] \\[10ex] = 16666.66667 * \left[\dfrac{0.09}{1 - \left(1 + 0.0075\right)^{-300}}\right] \\[7ex] = 16666.66667 * \left[\dfrac{0.09}{1 - \left(1.0075\right)^{-300}}\right] \\[7ex] = 16666.66667 * \left[\dfrac{0.09}{1 - 0.1062878338}\right] \\[5ex] = 16666.66667 * \left[\dfrac{0.09}{0.8937121662}\right] \\[5ex] = \dfrac{16666.66667 * 0.09}{0.8937121662} \\[5ex] = \dfrac{1500}{0.8937121662} \\[5ex] = 1678.392727 \\[3ex] PMT \approx \$1,678.39 \\[5ex] $ 2nd Approach: By Technology: Texas Instrument (TI) Finance App

Answer: Number21second

$ (b.) \\[3ex] Total\;\;Payment = Monthly\;\;Payment * Number\;\;of\;\;Months \\[3ex] = 1678.392727 * 25\;\;years * \dfrac{12\;months}{1\;year} \\[5ex] = 503517.8182 \\[3ex] \approx \$503517.82 \\[5ex] (c.) \\[3ex] Total\;\;Payment = \$503517.8182 \\[3ex] Principal = \$200000 \\[3ex] Interest = 503517.8182 - 200000 = \$303517.8182 \\[5ex] \underline{Percent:Proportion} \\[3ex] \dfrac{is}{of} = \dfrac{\%}{100} \\[5ex] What\;\;percent\;\;of\;\;503517.8182\;\;is\;\;200000? \\[3ex] \dfrac{200000}{503517.8182} = \dfrac{what}{100} \\[5ex] what = \dfrac{200000 * 100}{503517.8182} \\[5ex] what = 39.72054072\% \\[5ex] What\;\;percent\;\;of\;\;503517.8182\;\;is\;\;303517.8182? \\[3ex] \underline{1st\;\;Approach} \\[3ex] Total\;\;percent = 100\% \\[3ex] \implies \\[3ex] 100 - 39.72054072\% \\[3ex] = 60.27945928\% \\[5ex] \underline{2nd\;\;Approach:\;\;Percent:Proportion} \\[3ex] \dfrac{303517.8182}{503517.8182} = \dfrac{what}{100} \\[5ex] what = \dfrac{303517.8182 * 100}{503517.8182} \\[5ex] what = 60.27945928\% $