Processing math: 90%

Solved Examples: Arithmetic Operations on Measurements, Units, and Conversions

Pre-requisites:
(1.) Metric System
(2.) Customary System
(3.) All Measurements and Conversions

Samuel Dominic Chukwuemeka (SamDom For Peace)

For ACT Students
The ACT is a timed exam...60 questions for 60 minutes
This implies that you have to solve each question in one minute.
Some questions will typically take less than a minute a solve.
Some questions will typically take more than a minute to solve.
The goal is to maximize your time. You use the time saved on those questions you solved in less than a minute, to solve the questions that will take more than a minute.
So, you should try to solve each question correctly and timely.
So, it is not just solving a question correctly, but solving it correctly on time.
Please ensure you attempt all ACT questions.
There is no negative penalty for any wrong answer.

For JAMB and CMAT Students
Calculators are not allowed. So, the questions are solved in a way that does not require a calculator.

Solve all questions.
Use at least two methods as applicable.
State the measurement.
Show all work.

NOTE: Unless specified otherwise:
(1.) Use only the tables provided for you.
(2.) Please do not approximate intermediate calculations.
(3.) Please do not approximate final calculations. Leave your final answer as is.

Metric to Metric Conversions
Prefix	Symbol	Multiplication Factor
yocto	y	$10^{-24}$
zepto	z	$10^{-21}$
atto	a	$10^{-18}$
femto	f	$10^{-15}$
pico	p	$10^{-12}$
nano	n	$10^{-9}$
micro	$\mu$	$10^{-6}$
milli	m	$10^{-3}$
centi	c	$10^{-2}$
deci	d	$10^{-1}$
deka	da	$10^1$
hecto	h	$10^2$
kilo	K	$10^3$
mega	M	$10^6$
giga	G	$10^9$
tera	T	$10^{12}$
peta	P	$10^{15}$
exa	E	$10^{18}$
zetta	Z	$10^{21}$
yotta	Y	$10^{24}$

Customary to Customary Conversions
Measurement	Customary	Customary	Unit Conversion Factor
Length	inch (in)	foot (ft)	$12\:inches = 1\:ft$
Length	foot (ft)	yard (yd)	$3\:ft = 1\:yd$
Length	yard (yd)	mile (mi)	$1760\:yd = 1\:mi$
Length	foot (ft)	mile (mi)	$5280\:ft = 1\:mi$
Length	rod/pole	yards (yd)	$1\:rod = 5.5\:yd$
Length	furlong	rod	$1\:furlong = 40\;rod$
Length	fathom	feet (ft)	$1\:fathom = 6\;ft$
Length	league/marine	nautical miles	$1\:league = 3\;nautical\;\;miles$
Mass	pound (lb)	ounce (oz)	$1\:lb = 16\:oz$
Mass	short ton (ton)	pound (lb)	$1\:short\:ton = 2000\:lb$
Mass	long ton	pound (lb)	$1\:long\:ton = 2240\:lb$
Mass	stone	pound (lb)	$1\:\:stone = 14\:lb$
Mass	long ton	stone	$1\:long\:ton = 160\:stones$
Area	acre (acre)	square feet ( $ft^2$ )	$1\:acre = 43560\:ft^2$
Volume	quart (qt)	pint (pt)	$1\:qt = 2\:pt$
Volume	pint (pt)	cup (cup)	$1\:pt = 2\:cups$
Volume	quart (qt)	cup (cup)	$1\:qt = 4\:cups$
Volume	quart (qt)	fluid ounce (fl. oz)	$1\:qt = 32\:fl.\:oz$
Volume	pint (pt)	fluid ounce (fl. oz)	$1\:pt = 16\:fl.\:oz$
Volume	cup (cup)	fluid ounce (fl. oz)	$1\:cup = 8\:fl.\:oz$
Volume	gallon (gal)	quart (qt)	$1\:gal = 4\:qt$
Volume	gallon (gal)	quart (pt)	$1\:gal = 8\:pt$
Volume	gallon (gal)	cup (cup)	$1\:gal = 16\:cups$
Volume	gallon (gal)	fluid ounce (fl. oz)	$1\:gal = 128\:fl.\:oz$
Volume	gallon (gal)	cubic inches ( $in^3$ )	$1\:gal = 231\:in^3$

Metric to Customary Conversions
Measurement	Metric	Customary	Unit Conversion Factor
Length	meter (m)	foot (ft)	$1\:ft = 0.3048\:m$
Length	nautical miles	kilometer (km)	$1\:nautical\;\;mile = 1.852\;km$
Mass	gram (kg)	pound (lb)	$1\:lb = 453.59237\:g$
Mass	metric ton (tonne)	kilogram (kg)	$1\:tonne = 1000\:kg$
Volume	liter or cubic decimeters (L or $dm^3$ )	gallons (gal)	$1\:L = 0.26417205\:gal$

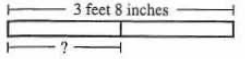
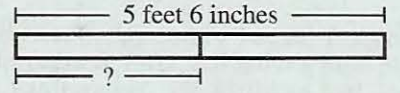
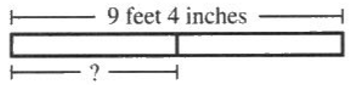
(1.) ACT Shown below, a board 9 feet 4 inches long is cut into 2 equal parts.
What is the length, to the nearest inch, of each part?

F. 4 feet 5 inches
G. 4 feet 7 inches
H. 4 feet 8 inches
J. 5 feet 4 inches
K. 5 feet 5 inches

We can do this question in at least two ways.
Use any method you prefer.
The first method is recommended for ACT

$\underline{First\:\:Method} \\[3ex] For:\:\:9\:feet\:\:\:4\:inches \\[3ex] First\:\:Step: \\[3ex] Divide\:\:the\:\:last\:\:unit(inches)\:\:by\:\:2...First\:\:Quotient \\[3ex] \dfrac{4\:inches}{2} = 2\:inches \\[5ex] Second\:\:Step: \\[3ex] Divide\:\:the\:\:first\:\:unit(feet)\:\:by\:\:2...Second\:\:Quotient \\[3ex] Then,\:\:convert\:\:any\:\:decimal\:\:part\:\:to\:\:inches \\[3ex] \dfrac{9\:feet}{2} = 4.5\:feet = 4\:feet + 0.5\:feet \\[5ex] 1\:foot = 12\:inches \\[3ex] 0.5\:foot = 0.5(12) = 6\:inches \\[3ex] Third\:\:Step: \\[3ex] Add\:\:the\:\:corresponding\:\:units\:\:from\:\:both\:\:quotients \\[3ex] 2\:inches + 6\:inches = 8\:inches \\[3ex] 0\:feet + 4\:feet = 4\:feet \\[3ex] \therefore \dfrac{9\:feet\:\:\:4\:inches}{2} = 4\:feet\:\:\:8\:inches \\[5ex] \underline{Second\:\:Method} \\[3ex] For:\:\:9\:feet\:\:\:4\:inches \\[3ex] First\:\:Step: \\[3ex] Convert\:\:to\:\:the\:\:last\:\:unit(inches) \\[3ex] 1\:foot = 12\:inches \\[3ex] 9\:feet = 9(12) = 108\:inches \\[3ex] 108\:inches + 4\:inches = 112\:inches \\[3ex] Second\:\:Step: \\[3ex] Divide\:\:the\:\:result\:\:by\:\:2 \\[3ex] \dfrac{112\:inches}{2} = 56\:inches \\[5ex] Third\:\:Step \\[3ex] Convert\:\:56\:\:inches\:\:to\:\:feet\:\:and\:\:inches \\[3ex] 12\:inches = 1\:foot \\[3ex] 56\:inches = \dfrac{56}{12} \\[5ex] = 4.66666667\:feet \\[3ex] = 4\:feet + 0.66666667\:feet \\[3ex] 0.66666667\:feet\:\:to\:\:inches \\[3ex] = 0.66666667(12) = 8\:inches \\[3ex] \therefore \dfrac{9\:feet\:\:\:4\:inches}{2} = 4\:feet\:\:\:8\:inches$

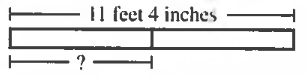
(2.) ACT Shown below, a board 11 feet 4 inches long is cut into 2 equal parts.
What is the length, to the nearest inch, of each part?

F. 5 feet 5 inches
G. 5 feet 7 inches
H. 5 feet 8 inches
J. 6 feet 5 inches
K. 6 feet 6 inches

We can do this question in at least two ways.
Use any method you prefer.
The first method is recommended for ACT

$\underline{First\:\:Method} \\[3ex] For:\:\:11\:feet\:\:\:4\:inches \\[3ex] First\:\:Step: \\[3ex] Divide\:\:the\:\:last\:\:unit(inches)\:\:by\:\:2...First\:\:Quotient \\[3ex] \dfrac{4\:inches}{2} = 2\:inches \\[5ex] Second\:\:Step: \\[3ex] Divide\:\:the\:\:first\:\:unit(feet)\:\:by\:\:2...Second\:\:Quotient \\[3ex] Then,\:\:convert\:\:any\:\:decimal\:\:part\:\:to\:\:inches \\[3ex] \dfrac{11\:feet}{2} = 5.5\:feet = 5\:feet + 0.5\:feet \\[5ex] 1\:foot = 12\:inches \\[3ex] 0.5\:foot = 0.5(12) = 6\:inches \\[3ex] Third\:\:Step: \\[3ex] Add\:\:the\:\:corresponding\:\:units\:\:from\:\:both\:\:quotients \\[3ex] 2\:inches + 6\:inches = 8\:inches \\[3ex] 0\:feet + 5\:feet = 5\:feet \\[3ex] \therefore \dfrac{11\:feet\:\:\:4\:inches}{2} = 5\:feet\:\:\:8\:inches \\[5ex] \underline{Second\:\:Method} \\[3ex] For:\:\:11\:feet\:\:\:4\:inches \\[3ex] First\:\:Step: \\[3ex] Convert\:\:to\:\:the\:\:last\:\:unit(inches) \\[3ex] 1\:foot = 12\:inches \\[3ex] 11\:feet = 11(12) = 132\:inches \\[3ex] 132\:inches + 4\:inches = 136\:inches \\[3ex] Second\:\:Step: \\[3ex] Divide\:\:the\:\:result\:\:by\:\:2 \\[3ex] \dfrac{136\:inches}{2} = 68\:inches \\[5ex] Third\:\:Step \\[3ex] Convert\:\:68\:\:inches\:\:to\:\:feet\:\:and\:\:inches \\[3ex] 12\:inches = 1\:foot \\[3ex] 68\:inches = \dfrac{68}{12} \\[5ex] = 5.66666667\:feet \\[3ex] = 5\:feet + 0.66666667\:feet \\[3ex] 0.66666667\:feet\:\:to\:\:inches \\[3ex] = 0.66666667(12) = 8\:inches \\[3ex] \therefore \dfrac{11\:feet\:\:\:4\:inches}{2} = 5\:feet\:\:\:8\:inches$

(3.) (a.) A storage pod has a rectangular floor that measures 23 feet by 9 feet and a flat ceiling that is 8 feet above the floor.
Find the area of the floor and the volume of the pod.

(b.) A lap pool has a length of 26 yards, a width of 23 yards, and a depth of 5 yards.
Find the pool's surface area (the water surface) and the total volume of water that the pool holds.

(c.) A raised flower bed is 40 feet long, 4 feet wide, and 1.8 feet deep.
Find the area of the bed and the volume of soil it holds.

Area = Length * Width
Volume = Length * Width * Depth
Volume = Length * Width * Height

$(a.) \\[3ex] \underline{Floor} \\[3ex] length = 23\;feet \\[3ex] width = 9\;feet \\[3ex] area = 23(9) \\[3ex] area = 207\;ft^2 \\[5ex] \underline{Pod} \\[3ex] height = 8\;feet \\[3ex] volume = 23(9)(8) \\[3ex] volume = 1656\;ft^3 \\[5ex] (b.) \\[3ex] \underline{Pool} \\[3ex] length = 26\;yards \\[3ex] width = 23\;yards \\[3ex] surface\;\;area = 26(23) \\[3ex] surface\;\;area = 598\;yard^2 \\[5ex] depth = 5\;yards \\[3ex] volume = 598(5) \\[3ex] volume = 2990\;yard^3 \\[5ex] (c.) \\[3ex] \underline{Flower\;\;Bed} \\[3ex] length = 40\;feet \\[3ex] width = 4\;feet \\[3ex] area = 40(4) \\[3ex] area = 160\;feet^2 \\[5ex] depth = 1.8\;feet \\[3ex] volume = 160(1.8) \\[3ex] volume = 288\;feet^3$

(4.) ACT Shown below, a board 3 feet 8 inches long is cut into 2 equal parts.
What is the length, to the nearest inch, of each part?

F. 1 foot 5 inches
G. 1 foot 8 inches
H. 1 foot 9 inches
J. 1 foot 10 inches
K. 2 feet 5 inches

We can do this question in at least two ways.
Use any method you prefer.
The first method is recommended for ACT

$\underline{First\:\:Method} \\[3ex] For:\:\:3\:feet\:\:\:8\:inches \\[3ex] First\:\:Step: \\[3ex] Divide\:\:the\:\:last\:\:unit(inches)\:\:by\:\:2...First\:\:Quotient \\[3ex] \dfrac{8\:inches}{2} = 4\:inches \\[5ex] Second\:\:Step: \\[3ex] Divide\:\:the\:\:first\:\:unit(feet)\:\:by\:\:2...Second\:\:Quotient \\[3ex] Then,\:\:convert\:\:any\:\:decimal\:\:part\:\:to\:\:inches \\[3ex] \dfrac{3\:feet}{2} = 1.5\:feet = 1\:feet + 0.5\:feet \\[5ex] 1\:foot = 12\:inches \\[3ex] 0.5\:foot = 0.5(12) = 6\:inches \\[3ex] Third\:\:Step: \\[3ex] Add\:\:the\:\:corresponding\:\:units\:\:from\:\:both\:\:quotients \\[3ex] 4\:inches + 6\:inches = 10\:inches \\[3ex] 0\:feet + 1\:feet = 1\:feet \\[3ex] \therefore \dfrac{3\:feet\:\:\:8\:inches}{2} = 1\:feet\:\:\:10\:inches \\[5ex] \underline{Second\:\:Method} \\[3ex] For:\:\:3\:feet\:\:\:8\:inches \\[3ex] First\:\:Step: \\[3ex] Convert\:\:to\:\:the\:\:last\:\:unit(inches) \\[3ex] 1\:foot = 12\:inches \\[3ex] 3\:feet = 3(12) = 36\:inches \\[3ex] 36\:inches + 8\:inches = 44\:inches \\[3ex] Second\:\:Step: \\[3ex] Divide\:\:the\:\:result\:\:by\:\:2 \\[3ex] \dfrac{44\:inches}{2} = 22\:inches \\[5ex] Third\:\:Step \\[3ex] Convert\:\:22\:\:inches\:\:to\:\:feet\:\:and\:\:inches \\[3ex] 12\:inches = 1\:foot \\[3ex] 22\:inches = \dfrac{22}{12} \\[5ex] = 1.83333333\:feet \\[3ex] = 1\:feet + 0.83333333\:feet \\[3ex] 0.83333333\:feet\:\:to\:\:inches \\[3ex] = 0.83333333(12) = 10\:inches \\[3ex] \therefore \dfrac{3\:feet\:\:\:8\:inches}{2} = 1\:feet\:\:\:10\:inches$

(5.) (a.) A warehouse is 63 yards long, 28 yards wide, and 8 yards high.
What is the area of the warehouse floor? If the warehouse is filled to half its height with tightly packed boxes, what is the volume of the boxes?

(b.) A room has a rectangular floor that measures 28 feet by 15 feet and a flat 8-foot ceiling.
What is the area of the floor and how much air does the room hold?

(c.) A grain silo has a circular base with an area of 260 square feet and is 19 feet tall.
What is the total volume?

Area = Length * Width
Volume = Length * Width * Depth
Volume = Length * Width * Height
Volume = Area * Height
How much air does the room hold ⇒ the Volume

$(a.) \\[3ex] \underline{Warehouse\;\;Floor} \\[3ex] length = 63\;yards \\[3ex] width = 28\;yards \\[3ex] area = 63(28) \\[3ex] area = 1764\;yard^2 \\[5ex] \underline{Warehouse} \\[3ex] height = \dfrac{1}{2}\;height = \dfrac{1}{2} * 8\;yards = 4\;yards \\[5ex] volume = 1764(4) \\[3ex] volume = 7056\;yard^3 \\[5ex] (b.) \\[3ex] \underline{Floor} \\[3ex] length = 28\;feet \\[3ex] width = 15\;feet \\[3ex] area = 28(15) \\[3ex] area = 420\;feet^2 \\[5ex] height = 8\;feet \\[3ex] volume = 420(8) \\[3ex] volume = 3360\;feet^3 \\[5ex] (c.) \\[3ex] \underline{Grain\;\;Silo} \\[3ex] area = 260\;feet^2 \\[5ex] height = 19\;feet \\[3ex] volume = 260(19) \\[3ex] volume = 4940\;feet^3$

(6.) ACT Shown below, a board 5 feet 6 inches long is cut into 2 equal parts.
What is the length, to the nearest inch, of each part?

A. 2 feet 5 inches
B. 2 feet 8 inches
C. 2 feet 9 inches
D. 3 feet 0 inches
E. 3 feet 5 inches

We can do this question in at least two ways.
Use any method you prefer.
The first method is recommended for ACT

$\underline{First\:\:Method} \\[3ex] For:\:\:5\:feet\:\:\:6\:inches \\[3ex] First\:\:Step: \\[3ex] Divide\:\:the\:\:last\:\:unit(inches)\:\:by\:\:2...First\:\:Quotient \\[3ex] \dfrac{6\:inches}{2} = 3\:inches \\[5ex] Second\:\:Step: \\[3ex] Divide\:\:the\:\:first\:\:unit(feet)\:\:by\:\:2...Second\:\:Quotient \\[3ex] Then,\:\:convert\:\:any\:\:decimal\:\:part\:\:to\:\:inches \\[3ex] \dfrac{5\:feet}{2} = 2.5\:feet = 2\:feet + 0.5\:feet \\[5ex] 1\:foot = 12\:inches \\[3ex] 0.5\:foot = 0.5(12) = 6\:inches \\[3ex] Third\:\:Step: \\[3ex] Add\:\:the\:\:corresponding\:\:units\:\:from\:\:both\:\:quotients \\[3ex] 3\:inches + 6\:inches = 9\:inches \\[3ex] 0\:feet + 2\:feet = 2\:feet \\[3ex] \therefore \dfrac{5\:feet\:\:\:6\:inches}{2} = 2\:feet\:\:\:9\:inches \\[5ex] \underline{Second\:\:Method} \\[3ex] For:\:\:5\:feet\:\:\:6\:inches \\[3ex] First\:\:Step: \\[3ex] Convert\:\:to\:\:the\:\:last\:\:unit(inches) \\[3ex] 1\:foot = 12\:inches \\[3ex] 5\:feet = 5(12) = 60\:inches \\[3ex] 60\:inches + 6\:inches = 66\:inches \\[3ex] Second\:\:Step: \\[3ex] Divide\:\:the\:\:result\:\:by\:\:2 \\[3ex] \dfrac{66\:inches}{2} = 33\:inches \\[5ex] Third\:\:Step \\[3ex] Convert\:\:33\:\:inches\:\:to\:\:feet\:\:and\:\:inches \\[3ex] 12\:inches = 1\:foot \\[3ex] 33\:inches = \dfrac{33}{12} \\[5ex] = 2.75\:feet \\[3ex] = 2\:feet + 0.75\:feet \\[3ex] 0.75\:feet\:\:to\:\:inches \\[3ex] = 0.75(12) = 9\:inches \\[3ex] \therefore \dfrac{5\:feet\:\:\:6\:inches}{2} = 2\:feet\:\:\:9\:inches$

Top